
Hyperbolsk paraboloid definisjon, egenskaper og eksempler

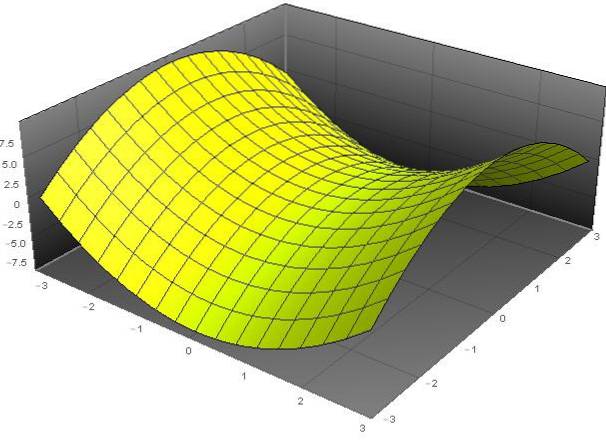
EN hyperbolsk paraboloid er en overflate hvis generelle ligning i kartesiske koordinater (x, y, z) oppfyller følgende ligning:
(til)to - (og / b)to - z = 0.
Navnet "paraboloid" kommer av det faktum at variabelen z avhenger av kvadratene til variablene x og y. Mens adjektivet "hyperbolsk" skyldes det faktum at ved faste verdier av z har vi ligningen til en hyperbol. Formen på denne overflaten ligner på en hestesadel.
Artikkelindeks
- 1 Beskrivelse av hyperbolsk paraboloid
- 2 Egenskaper til hyperbolsk paraboloid
- 3 Arbeidede eksempler
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 3.3 - Eksempel 3
- 4 Den hyperbolske paraboloid i arkitektur
- 5 Referanser
Beskrivelse av hyperbolsk paraboloid
For å forstå naturen til den hyperbolske paraboloid, vil følgende analyse bli gjort:
1.- Vi tar det spesielle tilfellet a = 1, b = 1, det vil si at den kartesiske ligningen av paraboloid forblir som z = xto - Yto.
2.- Planer parallelt med ZX-planet blir betraktet, det vil si y = ctte.
3.- Med y = ctte forblir det z = xto - C, som representerer paraboler med grener opp og toppunkt under XY-planet.
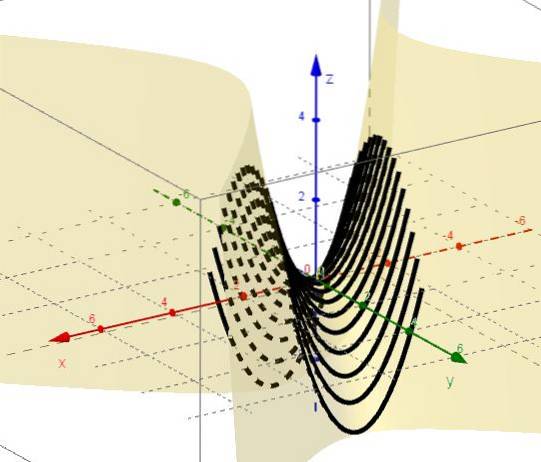
4.- Med x = ctte forblir det z = C - yto, som representerer paraboler med grener ned og toppunkt over XY-planet.
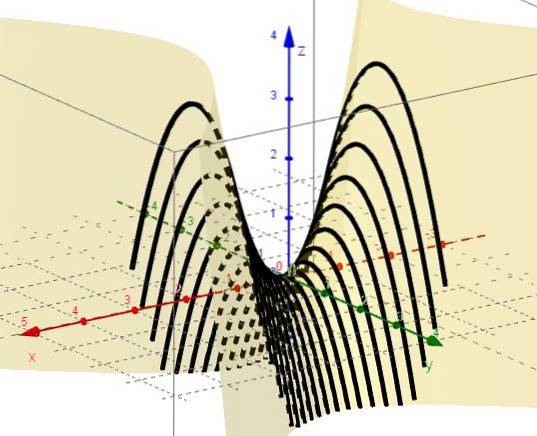
5.- Med z = ctte forblir det C = xto - Yto, som representerer hyperboler i plan parallelt med XY-planet. Når C = 0 er det to linjer (ved + 45º og -45 ° i forhold til X-aksen) som krysser ved opprinnelsen på XY-planet.
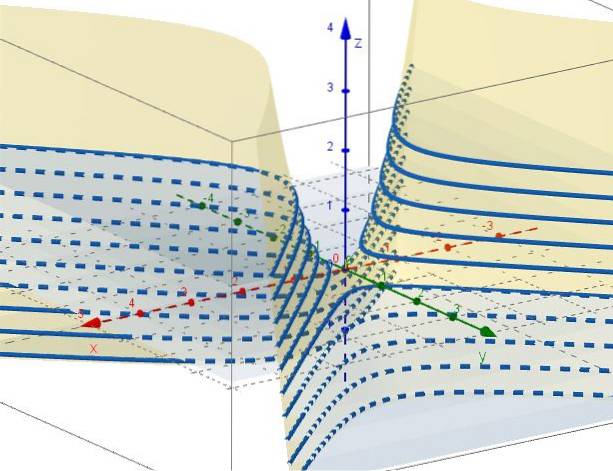
Egenskaper til hyperbolsk paraboloid
1.- Fire forskjellige punkter i tredimensjonalt rom definerer ett og bare ett hyperbolsk paraboloid.
2.- Den hyperbolske paraboloid er en dobbelt styrt overflate. Dette betyr at til tross for å være en buet overflate, passerer to forskjellige linjer gjennom hvert punkt i en hyperbolsk paraboloid som helt tilhører den hyperbolske paraboloid. Den andre overflaten som ikke er et plan og er dobbelt styrt er hyperboloid av revolusjon.
Det er nettopp den andre egenskapen til den hyperbolske paraboloid som har tillatt bred bruk i arkitektur siden overflaten kan genereres fra bjelker eller rette tau..
Den andre egenskapen til hyperbolsk paraboloid tillater en alternativ definisjon av den: er overflaten som kan genereres av en bevegelig rett linje parallelt med et fast plan og skjærer to faste linjer som fungerer som en guide. Følgende figur klargjør denne alternative definisjonen av hyperbolsk paraboloid:
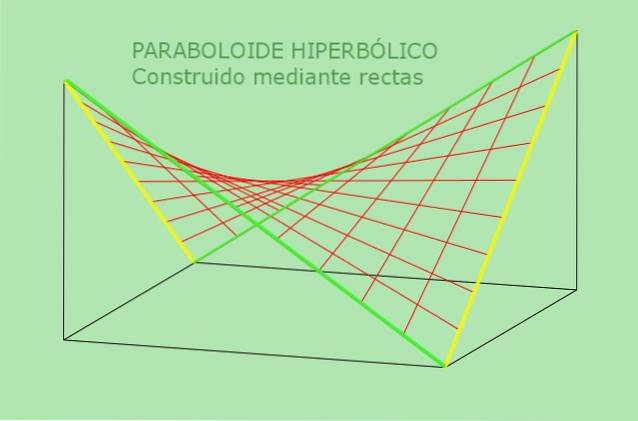
Arbeidet eksempler
- Eksempel 1
Vis at ligningen: z = xy, tilsvarer en hyperbolsk paraboloid.
Løsning
En transformasjon vil bli brukt på variablene x og y som tilsvarer en rotasjon av de kartesiske aksene i forhold til Z-aksen på + 45º. De gamle x- og y-koordinatene transformeres til de nye x 'og y' i henhold til følgende forhold:
x = x '- y'
y = x '+ y'
mens z-koordinaten forblir den samme, det vil si z = z '.
Ved å erstatte ligningen z = x og vi har:
z '= (x' - y ') (x' + y ')
Ved å bruke det bemerkelsesverdige produktet av forskjellen med summen som er forskjellen på kvadratene, har vi:
z '= x'to - Y 'to
som tilsvarer den opprinnelig definisjonen av hyperbolsk paraboloid.
Avskjæringen av flyene parallelt med XY-aksen med den hyperbolske paraboloid z = x og bestemmer likesidede hyperboler som har asymptotene flyene x = 0 og y = 0.
- Eksempel 2
Bestem parametrene til Y b av den hyperbolske paraboloid som passerer gjennom punktene A (0, 0, 0); B (1, 1, 5/9); C (-2, 1, 32/9) og D (2, -1, 32/9).
Løsning
I henhold til egenskapene bestemmer fire punkter i tredimensjonalt rom en enkelt hyperbolsk paraboloid. Den generelle ligningen er:
z = (x / a)to - (og / b)to
Vi erstatter de gitte verdiene:
For punkt A har vi 0 = (0 / a)to - (0 / b)to, ligning som er tilfredsstilt uansett verdiene til parametrene a og b.
Ved å erstatte punkt B får vi:
5/9 = 1 / ato - 1 Bto
Mens det for punkt C gjenstår:
32/9 = 4 / ato - 1 Bto
Til slutt, for punkt D får vi:
32/9 = 4 / ato - 1 Bto
Som er identisk med forrige ligning. Til slutt må ligningssystemet løses:
5/9 = 1 / ato - 1 Bto
32/9 = 4 / ato - 1 Bto
Å trekke den andre ligningen fra den første gir:
27/9 = 3 / ato som innebærer at ento = 1.
Tilsvarende blir den andre ligningen trukket fra firdoblingen til den første, og oppnår:
(32-20) / 9 = 4 / ato - 4 / ato -1 Bto + 4 / bto
Som er forenklet som:
12/9 = 3 / bto ⇒ bto = 9/4.
Kort fortalt har den hyperbolske paraboloid som passerer gjennom de gitte punktene A, B, C og D en kartesisk ligning gitt av:
z = xto - (4/9) ogto
- Eksempel 3
I henhold til egenskapene til det hyperbolske paraboloiden, passerer to linjer gjennom hvert punkt som er fullstendig inneholdt i det. For tilfellet z = x ^ 2 - y ^ 2 finn ligningen til de to linjene som går gjennom punktet P (0, 1, -1) som tydelig hører til den hyperbolske paraboloid, slik at alle punktene i disse linjene også hører til til det samme.
Løsning
Ved å bruke det bemerkelsesverdige produktet av forskjellen på kvadrater kan ligningen for hyperbolsk paraboloid skrives slik:
(x + y) (x - y) = c z (1 / c)
Hvor c er en ikke-null konstant.
Ligningen x + y = c z, og ligningen x - y = 1 / c tilsvarer to plan med normale vektorer n=<1,1,-c> Y m=<1,-1,0>. Vektorproduktet m x n =<-c, -c, -2> gir oss retningen på krysslinjen til de to planene. Så har en av linjene som går gjennom punktet P og tilhører den hyperbolske paraboloid en parametrisk ligning:
For å bestemme c erstatter vi punktet P i ligningen x + y = c z, og får:
c = -1
På en lignende måte, men med tanke på ligningene (x - y = k z) og (x + y = 1 / k), har vi den parametriske ligningen på linjen:
Oppsummert de to linjene:
De er fullstendig inneholdt i den hyperbolske paraboloid z = xto - Yto passerer gjennom punktet (0, 1, -1).
Anta som en sjekk, t = 1 som gir oss poenget (1,2, -3) på første linje. Du må sjekke om det også er på paraboloid z = xto - Yto:
-3 = 1to - toto = 1-4 = -3
Som bekrefter at det faktisk hører til overflaten av den hyperbolske paraboloid.
Den hyperbolske paraboloid i arkitektur

Det hyperbolske paraboloidet har blitt brukt i arkitekturen av de store avantgarde-arkitektene, blant hvilke navnene til den spanske arkitekten Antoni Gaudí (1852-1926) og særlig den også spanske Félix Candela (1910-1997) skiller seg ut..
Nedenfor er noen verk basert på hyperbolsk paraboloid:
-Kapell i byen Cuernavaca (Mexico) arbeidet til arkitekten Félix Candela.
-The Oceanographic of Valencia (Spania), også av Félix Candela.
Referanser
- Leksikon for matematikk. Regulert overflate. Gjenopprettet fra: encyclopediaofmath.org
- Llera Rubén. Hyperbolisk paraboloid. Gjenopprettet fra: rubenllera.wordpress.com
- Weisstein, Eric W. "Hyperbolic Paraboloid." Fra MathWorld-A Wolfram Web Resource. Gjenopprettet fra: mathworld.wolfram.com
- Wikipedia. Paraboloid. Gjenopprettet fra: en.wikipedia.com
- Wikipedia. Paraboloid. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Regulert overflate. Gjenopprettet fra: en.wikipedia.com



Ingen har kommentert denne artikkelen ennå.