Helling av en linjeformel og ligninger, representasjon, eksempler

De skråning av en linje er tangenten til vinkelen θ som linjen dannes med den horisontale aksen, som konvensjonelt måles mot urviseren. Helningen på en hvilken som helst linje er alltid konstant, og det er derfor den er en av dens viktigste egenskaper..

For å beregne det, må du vite to punkter på linjen, hvis koordinater er (x₁,Y₁) og (x_to,Y_to). Et segment som tilhører linjen tegnes mellom begge punkter, og deretter trekkes segmentene som representerer avstanden mellom x.₁ og x_to, og mellom og₁ og og_to, som i figuren nedenfor.

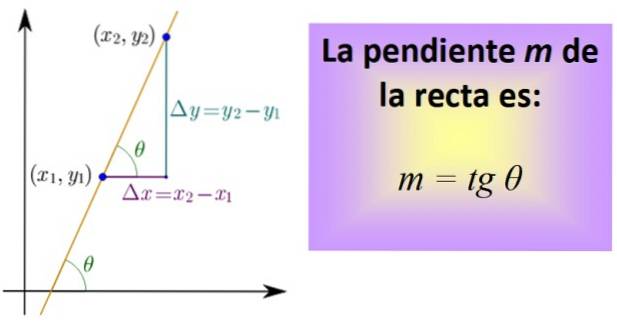
De tre segmentene utgjør en høyre trekant med bena: Δx = x_to - x₁  y Δy = y_to - Y₁. De tilsvarer henholdsvis en horisontal og en vertikal forskyvning..

Nå definerer vi et kvotient, kalt tangens til vinkelen θ og forkortet tg θ, som er nøyaktig stigningen m av den rette:

m = tg θ = Δy / Δx

Merk at for en linje forblir denne vinkelen konstant, uavhengig av punktene som er tatt for å beregne tangenten. Uansett gir denne verdien oss et mål på hvor bratt linjen er.

Gjennom koordinatene til de valgte punktene er formelen for skråningen:

m = (y - y₁ ) / (x_to - x₁)

Artikkelindeks

• 1 Grafisk fremstilling
• 2 Typer av skråning
• 3 Hvordan beregner du hellingen til en linje?
• 4 Løst øvelser
  • 4.1 - Øvelse 1
  • 4.2 - Øvelse 2
• 5 eksempler
  • 5.1 Eksempel 1
  • 5.2 Eksempel 2
• 6 Referanser

Grafisk fremstilling

Nedenfor har vi flere situasjoner der begrepet skråning er relevant. Verdien kan enkelt beregnes ved å måle den respektive vertikale og horisontale forskyvningen, og deretter gjøre kvotienten angitt i begynnelsen.

Dette gir oss en ide om ujevnheter eller tilbakegang av en eller annen struktur, for eksempel en rampe, et tak eller en vei:

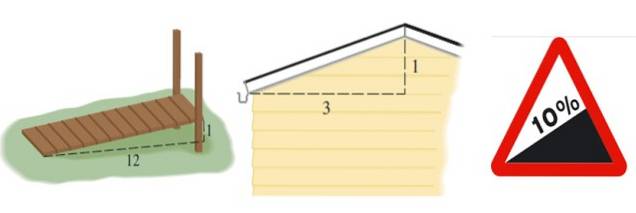
Skråningen til rampen vist i figur 2 til venstre er m = 1/12, takets er m = 1/3 og vegens uttrykkes i prosent. En prosentandel på 10% betyr at for hver 100 meter som går horisontalt, oppnås 10 meter i høyden:

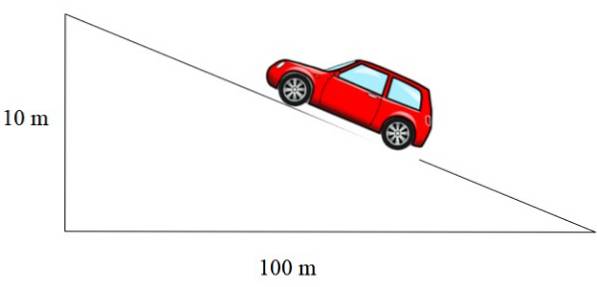
I dette tilfellet er hellingen 10/100 = 0,1, som, uttrykt i prosent, tilsvarer 10%..

Helningstyper

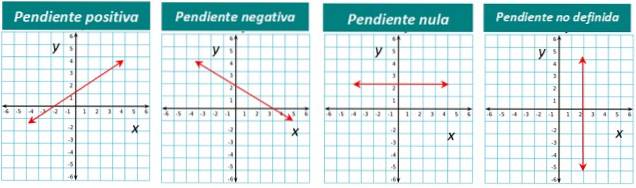
Helningen på en linje kan være positiv, negativ eller null. For eksempel har linjen vist i figur 1 en positiv skråning. Vi setter pris på det umiddelbart fordi vi ser at linjen "stiger" hvis vi ser den fra venstre til høyre.

Hvis linjen synker fra venstre til høyre, er skråningen negativ. Og når en linje er vannrett, er hellingen null.

Til slutt, for vertikale linjer, er skråningen ikke definert.

Den grafiske representasjonen av hver type er nedenfor:

Hvordan beregner du stigningen på en linje?

Beregning av skråningen er veldig enkel, du må bare finne den vertikale forskyvningen og den horisontale forskyvningen, og deretter lage kvotienten mellom begge.

Når vi har tegningen av linjen i det kartesiske planet, blir disse forskyvningene funnet ved å velge et hvilket som helst to punkter på linjen P₁ Og s_to, bestemme koordinatene og bruke definisjonen gitt i begynnelsen:

m = (y - y₁ ) / (x_to - x₁ )

Siden verdien på skråningen er uavhengig av valget av P₁ Og s_to , vi skal velge et punkt P hvilken som helst av koordinatene (x, y) som tilhører linjen, hvis koordinater ikke er kjent, og et annet punkt P₁ hvis koordinater er: (x₁,Y₁).

Skråningen er:

m = (y - y₁) / (x - x₁)

Vi kan fjerne Y:

og - og₁ = m (x - x₁)

Anta nå at punktet P₁ er skjæringspunktet mellom linjen og den vertikale aksen til koordinatene (0, b). Erstatter dette i ligningen ovenfor:

y - b = m (x - 0) → y = mx + b

Dette uttrykket er kjent som linjens ligning i formen skråning - avskjær, siden linjen utvetydig bestemmes når hellingen og skjæringspunktet med den vertikale aksen er kjent.

Å vite bare skråningen er ikke nok til å karakterisere en linje på flyet, siden uendelige linjer kan ha samme skråning, noe som betyr at de er parallelle, men går gjennom andre punkter.

Løst øvelser

- Øvelse 1

Finn hellingen til linjen vist i følgende figur:

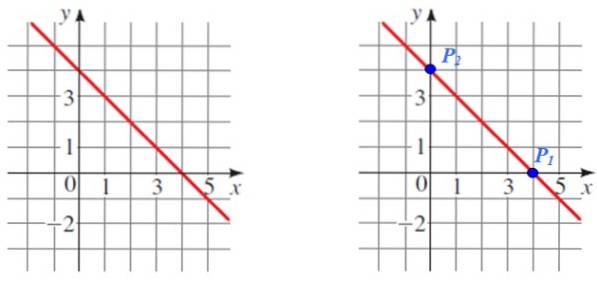
Løsning

P₁ Og s_to er to lettleste punkter som skal brukes til beregningen, legg også merke til at de er de respektive skjæringspunktene med koordinataksene.

Koordinatene til hvert punkt er:

P₁ (4.0) og P_to (0,4)

Ved å bytte ut ligningen for skråningen:

m = (4 - 0) / (0 - 4) = 4 / (- 4) = -1

Skråningen er negativ, noe som var å forvente etter å ha sett på grafen.

- Øvelse 2

Finn ligningen til linjen som går gjennom punktet (1, -6) og er parallell med linjen y = 2x - 3.

Løsning

Skråningen til den søkte linjen må være den samme som y = 2x - 3, siden de er parallelle. For denne linjen er hellingen m = 2, derfor har den vi leter etter formen:

og - og₁ = 2 (x - x₁)

Nå erstatter vi punktet som vår linje går gjennom: x₁ = 1 og y₁ = -6.

y - (-6) = 2 (x - 1)

Derfor er y = 2x - 2 - 6 → y = 2x - 8

Eksempler

To størrelser kan relateres på en slik måte at grafen deres er en rett linje. I så fall sies det at mengdene har lineær avhengighet, og linjens helning kan tolkes som endringshastigheten fra en variabel til den andre.

Eksempel 1

Anta at et basseng er fylt med vann ved en vurdere konstant i tid. Jo mer tid som går, jo mer lagres det naturlig. Vel, hastigheten bassenget fylles på er nøyaktig stigningen på linjen som relaterer volumet til tiden:

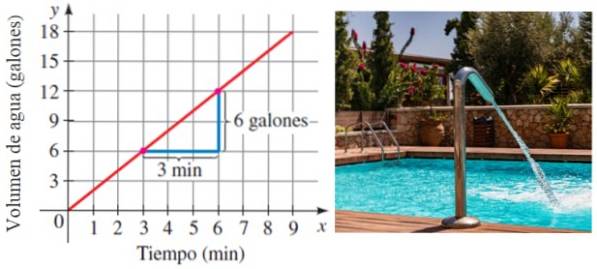
I dette eksemplet fylles bassenget med en hastighet på 6/3 liter per minutt eller 2 liter / minutt.

Eksempel 2

Når en mobil beveger seg i en rett linje med konstant hastighet, er hellingen til posisjonsgrafen som en funksjon av tiden ingen ringere enn nevnte hastighet. Grafen viser en mobil med positiv hastighet, noe som betyr at den beveger seg vekk fra opprinnelsen.

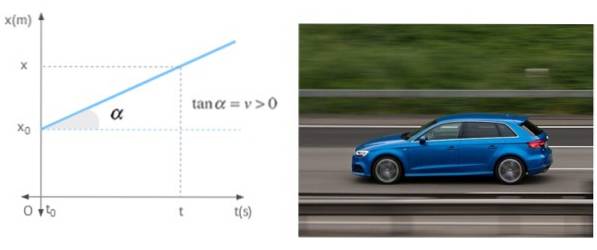
Referanser

1. Alvarez, J. Skråningen til en motorvei. Gjenopprettet fra: geogebra.es.
2. Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
3. Hoffman, J. Selection of Mathematics Topics. Volum 4.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Utgave. Cengage læring.
6. Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.