
Gage trykk forklaring, formler, ligninger, eksempler
De måler trykk Pm er det som måles i forhold til et referansetrykk, som i de fleste tilfeller er valgt som atmosfæretrykket Pminibank på havnivå. Det er da en relativt trykk, et annet begrep der det også er kjent.
Den andre måten man vanligvis måler trykk på er ved å sammenligne det med absolutt vakuum, hvis trykk alltid er null. I et slikt tilfelle snakker vi om absolutt press, som vi vil betegne som Ptil.
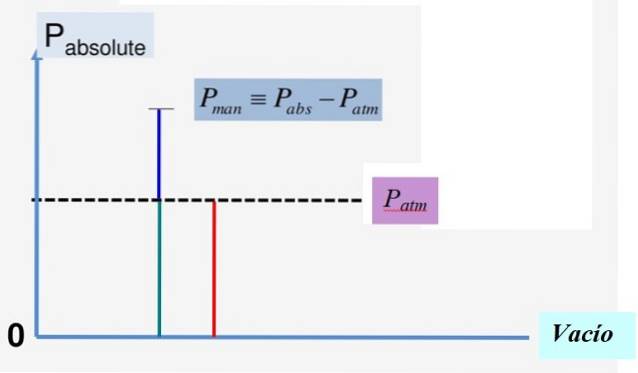
Det matematiske forholdet mellom disse tre størrelsene er:
Ptil = Pminibank + Pm
Derfor:
Pm = Ptil - Pminibank
Figur 1 illustrerer praktisk dette forholdet. Siden vakuumtrykket er 0, er det absolutte trykket alltid positivt, og det samme skjer med atmosfæretrykket Pminibank.
Målertrykk brukes ofte til å betegne trykk over atmosfæretrykk, slik som det som finnes i dekk eller det som er på bunnen av havet eller et svømmebasseng, som utøves av vekten av vannsøylen. I disse tilfellene Pm > 0, siden Ptil > Pminibank.
Imidlertid er det absolutt trykk under Pminibank. I disse tilfellene Pm < 0 y recibe el nombre de Press fra tømme og ikke forveksles med press av vakuum allerede beskrevet, som er fraværet av partikler som er i stand til å utøve trykk.
Artikkelindeks
- 1 Formler og ligninger
- 1.1 Variasjon av trykk med dybde
- 2 Eksempler
- 2.1 Pascals prinsipp
- 2.2 Stevins hydrostatiske paradoks
- 3 Øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referanser
Formler og ligninger
Trykket i en væske - væske eller gass - er en av de viktigste variablene i studien. I en stasjonær væske er trykket det samme på alle punkter i samme dybde uavhengig av orientering, mens bevegelsen av væsker i rørene er forårsaket av trykkendringer..
Gjennomsnittlig trykk er definert som kvotienten mellom kraften vinkelrett på en overflate F⊥ og arealet av overflaten A, som uttrykkes matematisk som følger:
P = F⊥ /TIL
Trykk er en skalar mengde, hvis dimensjoner er kraft per arealenhet. Enhetene til måling i International System of Units (SI) er newton / mto, kalt Pascal og forkortet som Pa, til ære for Blaise Pascal (1623-1662).
Flere som kilo (103) Y mega (106) blir ofte brukt, siden atmosfæretrykket vanligvis er i området 90 000 - 102 000 Pa, som er lik: 90 - 102 kPa. Trykk i størrelsesorden megapascal er ikke uvanlig, så det er viktig å bli kjent med prefikset.
I angelsaksiske enheter måles trykket i pund / fotto, imidlertid gjøres det vanligvis i pund / tommeto eller psi (pounds-force per kvadrattomme).
Trykkvariasjon med dybde
Jo mer vi fordyper oss i vannet i et basseng eller i havet, jo mer press opplever vi. Tvert imot, når høyden øker, reduseres atmosfæretrykket.
Det gjennomsnittlige atmosfæretrykket ved havnivå er etablert på 101,300 Pa eller 101,3 kPa, mens det i Mariana Trench i det vestlige Stillehavet - den dypeste kjente dybden - er omtrent 1000 ganger større og på toppen av Everest er det bare 34 kPa.
Det er tydelig at trykk og dybde (eller høyde) er relatert. For å finne ut i tilfelle væske i hvile (statisk likevekt), vurderes en skiveformet del av væske, begrenset i en beholder, (se figur 2). Skiven har tverrsnittsareal TIL, vekt dW og høyde dy.
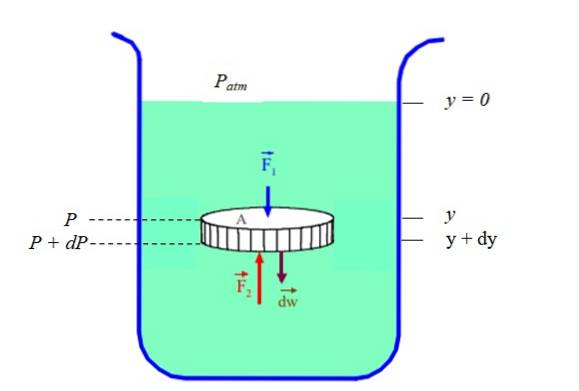
Vi vil ringe P til trykket som eksisterer på dybden "Y"Y P + dP til trykket som eksisterer på dybden (y + dy). Siden væskens tetthet ρ er forholdet mellom massen dm og volumet dV, du må:
ρ = dm / dV ⇒ dm = ρ.dV
Derfor vekten dW av elementet er:
dW = g. dm = ρ.g.dV
Og nå gjelder Newtons andre lov:
Σ FY = Fto - F1 - dW = 0
(P + dP) .A - P.A - ρ.g.dV = 0
(P + dP) .A - P.A - ρ.g. A. dy = 0
dP = ρ.g.dy
Løsning av differensiallikningen
Integrering av begge sider og med tanke på at tettheten ρ, så vel som tyngdekraften g er konstante, blir det søkte uttrykket funnet:
Pto - P1 = ΔP = ρ.g. (ogto - Y1)
ΔP = ρ.g. ΔY
Hvis du i forrige uttrykk velger P1 som atmosfærisk trykk og Y1 som overflaten av væsken, da Yto den ligger på en dybde h Y ΔP = Pto - Pminibank er målertrykket som en funksjon av dybde:
Pm = ρ.g.h
Hvis du trenger absolutt trykkverdi, kan du bare legge til atmosfæretrykket til forrige resultat.
Eksempler
For å måle målertrykket, ringte en enhet trykk måler, som generelt gir trykkforskjeller. På slutten vil arbeidsprinsippet til et U-rør manometer bli beskrevet, men la oss nå se på noen viktige eksempler og konsekvenser av den tidligere utledede ligningen.
Pascals prinsipp
Ligningen ΔP = ρ.g. (ogto - Y1) kan skrives som P = Po + ρ.g.h, hvor P er trykket på dybden h, samtidig som Peller er trykket på overflaten av væsken, vanligvis Pminibank.
Åpenbart hver gang det øker Po, øker P i samme mengde, så lenge det er en væske hvis tetthet er konstant. Det var nettopp det man skulle tenke på ρ konstant og plasser den utenfor integralen som ble løst i forrige avsnitt.
Pascals prinsipp sier at enhver økning i trykket til en begrenset væske i likevekt overføres uten noen variasjon til alle punkter i nevnte væske. Gjennom denne egenskapen er det mulig å multiplisere kraften F1 påført det lille stempelet til venstre, og få det Fto til høyre.
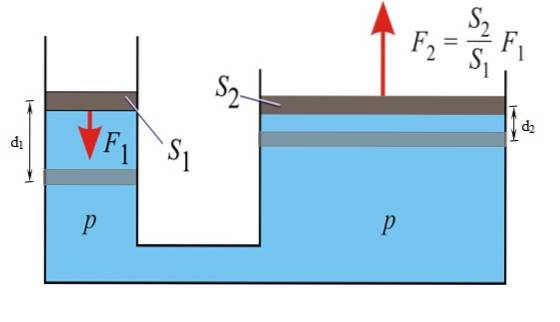
Bilbremser fungerer etter dette prinsippet: Det påføres en relativt liten kraft på pedalen, som blir en større kraft på bremsesylinderen ved hvert hjul, takket være væsken som brukes i systemet..
Stevins hydrostatiske paradoks
Det hydrostatiske paradokset sier at kraften på grunn av trykket til en væske i bunnen av en beholder kan være lik, større eller mindre enn vekten av selve væsken. Men når du setter beholderen på toppen av vekten, vil den normalt registrere vekten av væsken (pluss selvfølgelig beholderen til beholderen). Hvordan forklare dette paradokset?
Vi begynner med det faktum at trykket i bunnen av beholderen avhenger utelukkende av dybden og er uavhengig av formen, slik det ble utledet i forrige avsnitt.
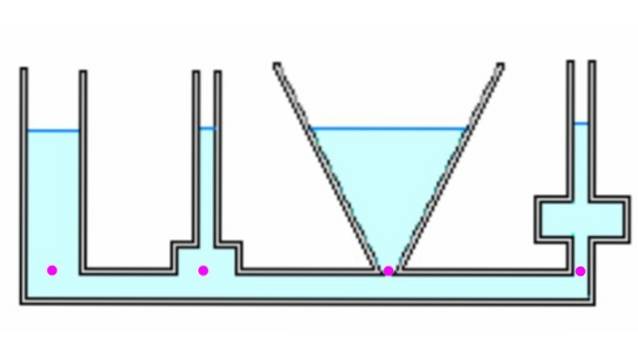
La oss se på noen få forskjellige containere. Når de blir kommunisert når de fylles med væske, når de alle samme høyde h. Høydepunktene har samme trykk, siden de er på samme dybde. Kraften på grunn av trykk ved hvert punkt kan imidlertid avvike fra vekten, (se eksempel 1 nedenfor).
Opplæring
Øvelse 1
Sammenlign kraften som utøves av trykket på bunnen av hver av beholderne med vekten av væsken, og forklar hvorfor forskjellene, hvis noen.
Beholder 1
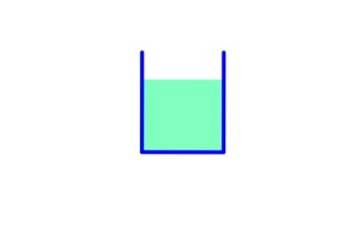
I denne beholderen er basisområdet A, derfor:
Væskevekt: mg = ρ.V.g = ρ . A .h. g
Trykk på bunnen: ρ. g. h
Kraft på grunn av trykk: F = P.A = ρ. g. h. TIL
Vekt og kraft på grunn av trykk er like.
Beholder 2
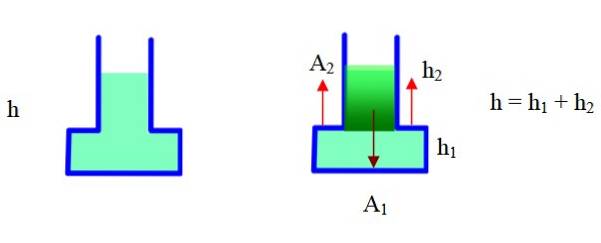
Containeren har en smal del og en bred del. I diagrammet til høyre er det delt inn i to deler, og geometri vil bli brukt til å finne det totale volumet. Område Ato Det er utvendig til containeren, hto er høyden på den smale delen, h1 er høyden på den brede delen (bunnen).
Fullt volum er volumet på basen + volumet på den smale delen. Med disse dataene har vi:
Væskevekt: m. g = ρ . g. V = ρ . g. [TIL1 .h1+ (TIL1 -TILto) .hto] =
= ρ . g (A1.hatohto) = ρ . g. TIL1.h - ρ . g. TIL.. hto (Bruk er gjort av h = h1 +hto)
Trykk på bunnen: P = ρ. g. h
Kraft på bunnen på grunn av trykk: F = P. A1 = ρ. g. h. TIL1
Å sammenligne vekten av væsken med kraften på grunn av trykk viser at dette er større enn vekten.
Det som skjer er at væsken også utøver kraft på den delen av trinnet i beholderen (se pilene i rødt på figuren) som er inkludert i beregningen ovenfor. Denne oppadgående kraften motvirker de som utøves nedover, og vekten registrert av skalaen er resultatet av disse. I henhold til dette er vektens størrelse:
W = Kraft på bunnen - Kraft på trinnet = ρ . g. TIL1.h - ρ . g. TIL.. hto
Øvelse 2
Et åpent rørmanometer er vist i figuren. Den består av et U-formet rør, hvor den ene enden er ved atmosfærisk trykk og den andre er koblet til S, systemet hvis trykk skal måles..
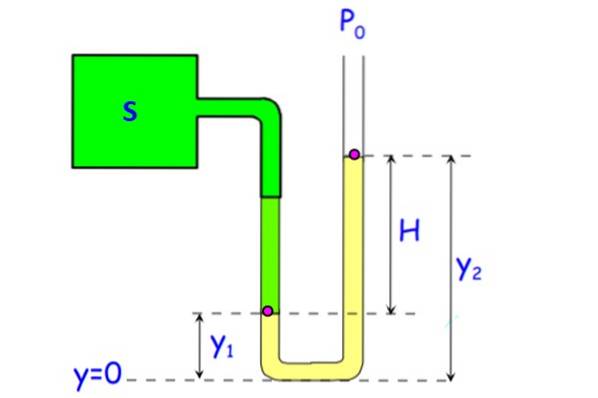
Væsken i røret (vist i gult på figuren) kan være vann, selv om kvikksølv fortrinnsvis brukes til å redusere størrelsen på enheten. (En forskjell på 1 atmosfære eller 101,3 kPa krever en 10,3 meter vannsøyle, ingenting bærbart).
Det ber om å finne målingstrykket Pm i system S, som en funksjon av høyden H på væskesøylen.
Løsning
Trykket i bunnen for begge grenene av røret er det samme, ettersom de er i samme dybde. La PTIL trykket ved punkt A, plassert ved y1 Og sB de i punkt B som er i høyden ogto. Siden punkt B er i grensesnittet mellom væske og luft, er trykket der Peller. I denne grenen av manometeret er trykket nederst:
Po + ρ.g.yto
For sin del er trykket nederst for grenen til venstre:
P + ρ.g.y1
Hvor P er det absolutte trykket i systemet og ρ er densiteten til væsken. Utjevner begge trykk:
Po + ρ.g.yto = P + ρ.g.y1
Rydding ut P:
P = Po + ρ.g.yto - ρ.g.y1 = Po + ρ.g (ogto - Y1) = Po + ρ.g. H
Derfor måler trykket Pm er gitt av P - Peller = ρ.g. H og for å ha verdien, måler du bare høyden som den manometriske væsken stiger til og multipliserer den med verdien av g og væskens tetthet.
Referanser
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volum 4. Væsker og termodynamikk. Redigert av Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Væskemekanikk. 4. plass Utgave. Pearson Education. 53-70.
- Shaugnessy, E. 2005. Introduksjon til væskemekanikk. Oxford University Press. 51 - 60.
- Stylianos, V. 2016. En enkel forklaring på det klassiske hydrostatiske paradokset. Gjenopprettet fra: haimgaifman.files.wordpress.com



Ingen har kommentert denne artikkelen ennå.