
Assosiativ egenskapstilsetning, multiplikasjon, eksempler, øvelser
De tilknytningseiendom av summen representerer den assosiative karakteren til sumoperasjonen i forskjellige matematiske sett. I den er tre (eller flere) elementer av disse settene relatert, kalt a, b og c, slik at det alltid er sant:
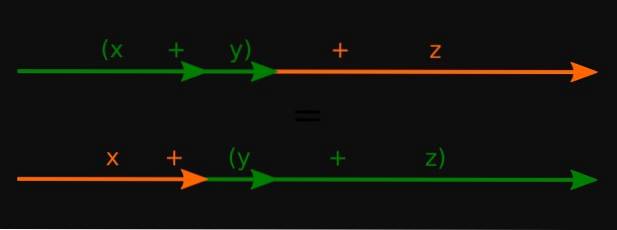
a + (b + c) = (a + b) + c
På denne måten er det garantert at uansett grupperingsmåte for å gjennomføre operasjonen, blir resultatet det samme.

Men det skal bemerkes at den assosiative egenskapen ikke er synonymt med kommutativ egenskap. Det vil si at vi vet at rekkefølgen på tilleggene ikke endrer summen, eller at rekkefølgen på faktorene ikke endrer produktet. Så for summen kan det skrives slik: a + b = b + a.
Imidlertid er det i den assosiative egenskapen annerledes, siden rekkefølgen på elementene som skal legges til, opprettholdes og det som endres er operasjonen som utføres først. Hvilket betyr at det ikke betyr noe å legge til først (b + c) og til dette resultatet legge til a, enn å begynne å legge til a med b og til resultatet legge til c.
Mange viktige operasjoner som tillegg er assosiative, men ikke alle. For eksempel i subtraksjon av reelle tall skjer det at:
a - (b - c) ≠ (a - b) - c
Hvis a = 2, b = 3, c = 1, så:
2- (3 - 1) ≠ (2-3) - 1
0 ≠ -2
Artikkelindeks
- 1 Assosiativ egenskap for multiplikasjon
- 1.1 Anvendelser av den assosiative egenskapen til multiplikasjon
- 2 Eksempler
- 2.1 Den assosiative egenskapen i vektorer
- 2.2 Faktorisering av polynomer ved gruppering av termer
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referanser
Assosiativ egenskap for multiplikasjon
Som det ble gjort for tillegg, sier den assosiative egenskapen til multiplikasjon at:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
Når det gjelder settet med reelle tall, er det enkelt å verifisere at dette alltid er tilfelle. For eksempel bruker vi verdiene a = 2, b = 3, c = 1, har vi:
to ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Reelle tall oppfyller den assosiative egenskapen til både addisjon og multiplikasjon. På den annen side, i et annet sett, slik som for vektorer, er summen assosiativ, men kryssproduktet eller vektorproduktet er det ikke..
Anvendelser av den assosiative egenskapen til multiplikasjon
En fordel med operasjoner der den tilknyttede eiendommen oppfylles, er å kunne gruppere på den mest praktiske måten. Dette gjør oppløsningen mye enklere..
Anta for eksempel at det i et lite bibliotek er 3 hyller med 5 hyller hver. I hver hylle er det 8 bøker. Hvor mange bøker er det totalt?
Vi kan utføre operasjonen slik: totalt bøker = (3 x 5) x 8 = 15 x 8 = 120 bøker.
Eller slik: 3 x (5 x 8) = 3 x 40 = 120 bøker.

Eksempler
-I settene med naturlige, heltall, rasjonelle, reelle og komplekse tall blir den assosiative egenskapen til addisjon og multiplikasjon oppfylt.
-For polynomer gjelder også i disse operasjonene.
-I tilfeller av operasjoner med subtraksjon, divisjon og eksponentiering, oppfylles ikke den tilknyttede eiendommen verken i reelle tall eller i polynomer..
-Når det gjelder matriser, holder den assosiative egenskapen for tillegg og multiplikasjon, selv om kommutativitet ikke er oppfylt i sistnevnte tilfelle. Dette betyr at gitt matriser A, B og C er det sant at:
(A x B) x C = A x (B x C)
Men ... A x B ≠ B x A
Den assosiative egenskapen i vektorer
Vektorer danner et annet sett enn reelle tall eller komplekse tall. Operasjonene som er definert for settet med vektorer er noe forskjellige: det er addisjon, subtraksjon og tre typer produkter.
Summen av vektorer oppfyller den assosiative egenskapen, det samme gjør tall, polynomer og matriser. Når det gjelder skalarproduktene, skalar etter vektor og kryss som er laget mellom vektorer, oppfyller sistnevnte det ikke, men skalarproduktet, som er en annen type operasjon mellom vektorer, oppfyller det, med tanke på følgende:
-Produktet av en skalar og en vektor resulterer i en vektor.
-Og når du skalar multipliserer to vektorer, blir det en skalar.
Derfor gitt vektorene v, eller Y w, og i tillegg en skalar λ, er det mulig å skrive:
-Summen av vektorer: v +(eller + w ) = (v + eller) + w
-Skalarprodukt: λ (v • eller ) = (λv) • eller
Sistnevnte er mulig takket være v • eller resulterer i en skalar, og λv det er en vektor.
Derimot:
v × (eller × w ) ≠ (v × eller)×w
Faktorisering av polynomer ved gruppering av termer
Denne applikasjonen er veldig interessant, for som det ble sagt tidligere, hjelper den assosiative egenskapen til å løse visse problemer. Summen av monomer er assosiativ, og dette kan brukes til å faktorere når en åpenbar felles faktor ikke vises ved første øyekast.
Anta for eksempel at du ber om å faktorere: x3 + toxto + 3x +6. Dette polynomet har ingen felles faktor, men la oss se hva som skjer hvis det er gruppert slik:
x3 + 2xto + 3x +6 = (x3 + 2xto) + (3x +6)
Den første parentesen har som en felles faktor xto:
x3 + toxto = xto (x + 2)
I det andre er den vanlige faktoren 3:
3x +6 = 3 (x + 2)
Deretter:
x3 + toxto + 3x +6 = xto(x + 2) + 3 (x + 2)
Nå er det en åpenbar felles faktor, som er x + 2:
xto(x + 2) + 3 (x + 2) = (x + 2) (xto+3)
Opplæring
- Øvelse 1
En skolebygning har 4 etasjer og hver har 12 klasserom med 30 skrivebord inne. Hvor mange pulter har skolen totalt?
Løsning
Dette problemet løses ved å bruke den assosiative egenskapen til multiplikasjon, la oss se:
Totalt antall pulter = 4 etasjer x 12 klasserom / etasje x 30 pulter / klasserom = (4 x 12) x 30 pulter = 48 x 30 = 1440 pulter.
Eller hvis du foretrekker det: 4 x (12 x 30) = 4 x 360 = 1440 skrivebord
- Øvelse 2
Gitt polynomene:
A (x) = 5x3 + 2xto -7x + 1
B (x) = x4 +6x3 -5x
C (x) = -8xto +3x -7
Bruk den assosiative egenskapen til tillegg for å finne A (x) + B (x) + C (x).
Løsning
Du kan gruppere de to første og legge til den tredje i resultatet:
A (x) + B (x) = [5x3 + 2xto -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2xto -12x +1
Umiddelbart tilsettes polynomet C (x):
[x4 + 11x3+ 2xto -12x +1] + [-8xto +3x -7] = x4 + 11x3 - 6xto -9x -6
Leseren kan verifisere at resultatet er identisk hvis det løses ved hjelp av alternativet A (x) + [B (x) + C (x)].
Referanser
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematikk er morsom. Kommuterende, assosierende og fordelende lover Gjenopprettet fra: mathisfun.com.
- Matematikklager. Definisjon av tilknyttet eiendom. Gjenopprettet fra: mathwarehouse.com.
- Vitenskapelig. Assosiativ og kommutativ egenskap for tillegg og multiplikasjon (med eksempler). Gjenopprettet fra: sciencing.com.
- Wikipedia. Assosiativ eiendom. Gjenopprettet fra: en.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.