
Lås egenskap for algebra bevis, eksempler
De låseegenskap av algebra er et fenomen som relaterer to elementer i et sett med en operasjon, der den nødvendige forutsetningen er at etter at de to elementene er behandlet under nevnte operasjon, hører resultatet også til det første sett.
For eksempel, hvis partall blir tatt som et sett og en sum som en operasjon, får vi en lås av det settet med hensyn til summen. Dette er fordi summen av 2 partall alltid vil gi et annet partall, og dermed oppfylle låsebetingelsen.

Artikkelindeks
- 1 Funksjoner
- 2 Antall algebra
- 3 Demo
- 3.1 Sum
- 3.2 Multiplikasjon
- 4 Spesielle tilfeller i R
- 4.1 Divisjon
- 4.2 Arkivering
- 4.3 Logaritme
- 5 eksempler
- 5.1 Sum i N
- 5.2 Subtraksjon i N
- 6 Forslag til øvelser
- 7 Referanser
Kjennetegn
Det er mange egenskaper som bestemmer algebraiske rom eller kropper, for eksempel strukturer eller ringer. Låseiendommen er imidlertid en av de mest kjente innen grunnleggende algebra.
Ikke alle anvendelser av disse egenskapene er basert på numeriske elementer eller fenomener. Mange hverdagseksempler kan bearbeides ut fra en ren algebraisk-teoretisk tilnærming.
Et eksempel kan være borgere i et land som påtar seg et juridisk forhold av noe slag, for eksempel et kommersielt partnerskap eller ekteskap blant andre. Etter at denne operasjonen eller ledelsen er utført, forblir de statsborgere i landet. På denne måten representerer statsborgerskap og ledelse med to borgere en lås.
Numerisk algebra
Når det gjelder tall, er det mange aspekter som har vært gjenstand for studier i forskjellige strømninger av matematikk og algebra. Et stort antall aksiomer og teoremer har kommet frem fra disse studiene som tjener som det teoretiske grunnlaget for moderne forskning og arbeid..
Hvis vi jobber med de numeriske settene, kan vi etablere en annen gyldig definisjon for låseegenskapen. Et sett A sies å være låsen til et annet sett B hvis A er det minste settet som inneholder alle settene og operasjonene som B huser..
Demonstrasjon
Låsesikkerheten brukes for elementer og operasjoner som er tilstede i settet med reelle tall R.
La A og B være to tall som hører til mengden R, lukkingen av disse elementene er definert for hver operasjon inneholdt i R.
Sum
- Sum: ∀ A ˄ B ∈ R → A + B = C ∈ R
Dette er den algebraiske måten å si det på For alle A og B som tilhører reelle tall, har vi at summen av A pluss B er lik C, som også tilhører de reelle tallene.
Det er lett å sjekke om denne proposisjonen stemmer; det er nok å utføre summen mellom et hvilket som helst reelt tall og sjekke om resultatet også tilhører de reelle tallene.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 ∈ R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Det observeres at låsebetingelsen er oppfylt for de reelle tallene og summen. På denne måten kan det konkluderes: Summen av reelle tall er en algebraisk lås.
Multiplikasjon
- Multiplikasjon: ∀ A ˄ B ∈ R → A. B = C ∈ R
For alle A og B som tilhører realene, har vi at multiplikasjonen av A med B er lik C, som også tilhører realene.
Når du verifiserer med de samme elementene i forrige eksempel, observeres følgende resultater.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ∈ R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Dette er nok bevis for å konkludere med at: Multiplikasjon av reelle tall er en algebraisk lås.
Denne definisjonen kan utvides til alle operasjoner på reelle tall, selv om vi finner visse unntak.

Spesielle tilfeller i R
Inndeling
Som det første spesielle tilfellet observeres delingen, der følgende unntak observeres:
∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0
For alle A og B som tilhører R vi har at A blant B ikke tilhører realene hvis og bare hvis B er lik null.
Denne saken viser til begrensningen av å ikke kunne dele med null. Siden null hører til de reelle tallene, konkluderes det med at: lInndelingen er ikke en lås på realen.
Arkivering
Det er også potensieringsoperasjoner, nærmere bestemt de fra radikalisering, der unntak presenteres for radikale krefter med jevn indeks:
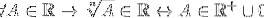
For alle A som tilhører realene, tilhører den nte roten til A realene, hvis og bare hvis A tilhører de positive realene som er koblet til et sett hvis eneste element er null.
På denne måten betegnes det at de jevne røttene bare gjelder for positive realer, og det konkluderes med at potensiering ikke er en lås i R.
Logaritme
På en homolog måte kan det sees for den logaritmiske funksjonen, som ikke er definert for verdier mindre enn eller lik null. For å sjekke om logaritmen er en lås av R, gjør du slik:
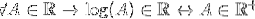
For alle A som tilhører realene, tilhører logaritmen til A realene, hvis og bare hvis A tilhører de positive realene.
Ved å ekskludere negative verdier og null som også tilhører R, kan det sies at:
Logaritmen er ikke en lås av de reelle tallene.
Eksempler
Sjekk låsen for tillegg og subtraksjon av naturlige tall:
Sum i N
Det første er å sjekke låsetilstanden for forskjellige elementer i det gitte settet. Hvis det blir observert at noe element bryter med tilstanden, kan eksistensen av en lås automatisk nektes.
Denne egenskapen gjelder for alle mulige verdier av A og B, som observert i følgende operasjoner:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
Det er ingen naturlige verdier som bryter låseforholdet, så det konkluderes:
Summen er en lås i N.
Trekk i N
De leter etter naturlige elementer som er i stand til å bryte tilstanden; A - B tilhører de innfødte.
Det er enkelt å finne par naturlige elementer som ikke oppfyller låseforholdene. For eksempel:
7 - 10 = -3 ∉ a N
På denne måten kan vi konkludere med at:
Subtraksjon er ikke en lås av settet med naturlige tall.
Foreslåtte øvelser
1-Vis om låseegenskapen er oppfylt for settet med rasjonelle tall Q, for operasjonstilsetning, subtraksjon, multiplikasjon og divisjon.
2-Forklar om settet med reelle tall er en lås av settet med heltall.
3-Bestem hvilket numerisk sett som kan være låsing av de reelle tallene.
4-Bevis låseegenskapen for settet med imaginære tall, med hensyn til addisjon, subtraksjon, multiplikasjon og divisjon.
Referanser
- Panorama over ren matematikk: det Bourbakistiske valget. Jean Dieudonné. Reverte, 1987.
- Algebraisk tallteori. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
- Lineær algebra og dets applikasjoner. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Algebraiske strukturer V: kroppsteori. Hector A. Merklen. Organization of American States, Generalsekretariat, 1979.
- Introduksjon til kommutativ algebra. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.



Ingen har kommentert denne artikkelen ennå.