
Kartografiske kjegleprojeksjonsegenskaper, fordeler, ulemper
De kartografisk konisk projeksjon Det er preget av å projisere punktene på en sfærisk overflate på overflaten av en kjegle, hvis toppunkt er plassert på aksen som går gjennom polene og er tangent eller sekant til sfæren. Kjeglen er en overflate som kan åpnes i et plan og danner en vinkelsektor uten å deformere linjene som er projisert på den..
Matematikeren Johann Heinrich Lambert (1728 - 1777) var den som utviklet denne projeksjonen, og dukket opp for første gang i sin bok Freye Perspective (1759), hvor han samlet ulike teorier og refleksjoner over anslag.
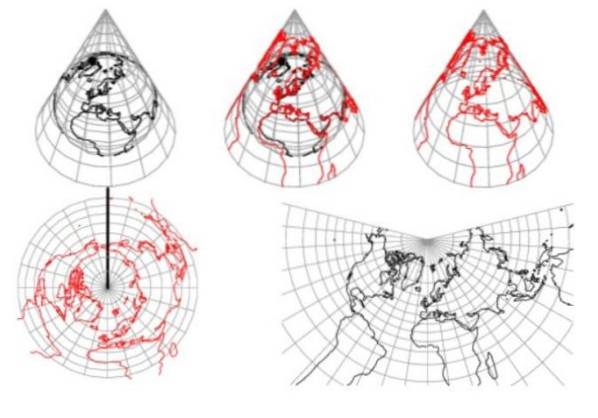
I koniske fremspring på jordoverflaten blir meridianene radiale linjer sentrert på toppunktet, med like vinkelavstand, og de jordiske parallellene blir sirkelbuer konsentriske til toppunktet.
Figur 1 viser at den koniske projeksjonen ikke tillater å representere begge halvkuler. I tillegg observeres det tydelig at avstandene er forvrengt vekk fra parallellene som fanger opp kjeglen.
Av disse grunner brukes denne typen projeksjon til å representere regioner med mellombreddegrad, omfattende fra øst til vest og i mindre nord-sørlig grad. Slik er tilfellet i det kontinentale USA.
Artikkelindeks
- 1 Fordeler
- 1.1 Den like avstandige koniske projeksjonen
- 2 Albert's koniske projeksjon
- 3 Lambert Conformal Conic Projection
- 4 Referanser
Fordel
Jorden kan tilnærmes til en kule med en radius på 6378 km, med tanke på at alle land- og vannmassene er på den store sfæren. Det handler om å konvertere denne overflaten, som dekker et objekt i tre dimensjoner, for eksempel en kule, til et annet objekt i to dimensjoner: et flatt kart. Dette medfører ulempen at den buede overflaten er forvrengt når du ønsker å projisere den på flyet.
Kartprojeksjoner, som konisk projeksjon, prøver å løse dette problemet med så lite tap av nøyaktighet som mulig. Derfor er det flere alternativer for å lage en projeksjon, avhengig av egenskapene du vil fremheve..
Blant disse viktige egenskapene er avstander, overflate, vinkler og mer. Den beste måten å bevare dem alle på er å representere Jorden i 3D for å skalere. Men dette er ikke alltid praktisk.
Å bære en klode overalt er ikke lett, da det tar opp volum. Du kan heller ikke se hele jordoverflaten på en gang, og det er umulig å reprodusere alle detaljene på en skalamodell..
Vi kan forestille oss at planeten er en appelsin, vi skreller appelsinen og sprer skallet på bordet og prøver å rekonstruere bildet av appelsinens overflate. Det er klart at mye informasjon vil gå tapt i prosessen.
Projiseringsalternativene er som følger:
- Projiser på et fly eller
- På en sylinder, som kan utvikles som et rektangulært plan.
- Endelig på en kjegle.
Det koniske projeksjonssystemet har fordelen at det er nøyaktig i forhold til parallellene som er valgt for å fange opp projeksjonskeglen..
I tillegg holder det orientering langs meridianene praktisk talt intakt, selv om det kan forvride skalaen langs meridianene noe for breddegrader langt fra standard- eller referanseparalleller. Derfor er det hensiktsmessig å representere veldig store land eller kontinenter.
Den like langt koniske projeksjonen
Det er det koniske projeksjonssystemet som opprinnelig ble brukt av Ptolemaios, en gresk geograf som bodde mellom 100-170 e.Kr. Senere i 1745 ble den forbedret.
Det brukes ofte i atlasser i regioner med mellomliggende breddegrader. Den er egnet for å vise områder med noen få breddegrader, og som tilhører en av ekvatoriale halvkuler.
I denne projeksjonen er avstandene sanne langs meridianene og i de to standardparallellene, det vil si parallellene som er valgt for å fange opp med projeksjonskeglen..
I den like avstandige koniske projeksjonen strekker et punkt på sfæren seg radielt til det krysser seg med tangent- eller sekantkeglen, og tar senterets sentrum som projeksjonssenteret..
Ulemper
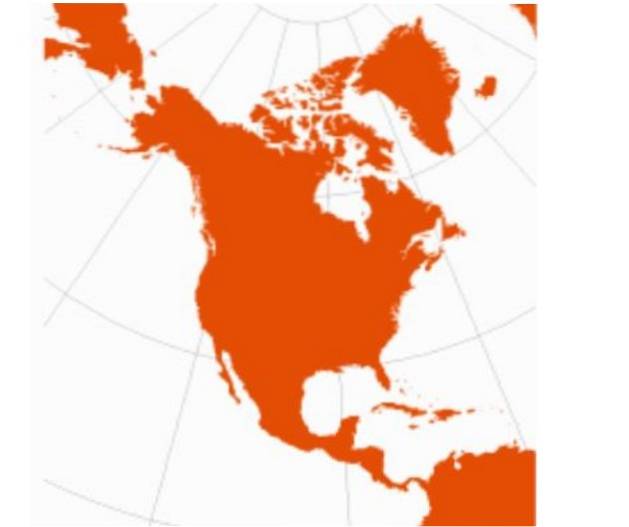
Den største ulempen med konisk projeksjon er at den ikke gjelder for ekvatoriale regioner.
I tillegg er konisk projeksjon ikke hensiktsmessig for å kartlegge store regioner, men heller bestemte områder, som Nord-Amerika..
Albert's koniske projeksjon
Bruk to standardparalleller og bevar arealet, men ikke skala og form. Denne typen konisk projeksjon ble introdusert av H. C. Albers i 1805.
Alle områdene på kartet er proporsjonale med områdene på jorden. I begrensede regioner er retningen relativt nøyaktig. Avstandene tilsvarer de på den sfæriske overflaten på standardparallellene.
I USA brukes dette projeksjonssystemet til kart som viser grensene for Unionens stater, for hvilke 29,5 º N og 45,5 º N er valgt som standardparalleller, noe som resulterer i en maksimal skalafeil på 1, 25%.
Kart laget med denne projeksjonen bevarer ikke vinklene som tilsvarer kulens, og de bevarer heller ikke perspektiv eller like stor avstand.
Lambert Conformal Conic Projection
Det ble foreslått i 1772 av den sveitsiske matematikeren og geografen med samme navn. Hovedkarakteristikken er at den bruker en kjegl tangens eller sekant til sfæren og projeksjonen holder vinklene uforanderlige. Disse egenskapene gjør det veldig nyttig i luftfartsnavigasjonskart..
United States Geological Survey (USGS) bruker projeksjonen Lambert Conic. I denne projeksjonen er avstandene sanne langs standardparallellene.

I Lambert-konisk projeksjon forblir retningene rimelig presise. Områdene og formene er litt forvrengt i posisjoner nær standardparallellene, men endring av form og areal øker med separasjon til dem..
Fordi målet med denne projeksjonen er å opprettholde retninger og vinkler som er like originale på sfæren eller ellipsoiden, er det ingen geometrisk metode for å oppnå den, i motsetning til den like store projeksjonen til Ptolemaios..
Snarere er det en analytisk projeksjonsmetode, basert på matematiske formler.
USGS basiskart for de 48 kontinentale statene bruker 33ºN og 45ºN som standardparalleller, noe som gir en maksimal kartfeil på 2,5%..
For navigasjonskart i Alaska er basisparallellene 55ºN og 65ºN. I stedet bruker det nasjonale atlaset i Canada 49ºN og 77ºN.
Referanser
- Geohunter. Lambert Conformal Conic-projeksjonen. Gjenopprettet fra: geo.hunter.cuny.edu
- Gisgeography. Konisk projeksjon: Lambert, Albers og Polyconic. Gjenopprettet fra: gisgeography.com
- Gisgeography. Hva er kartprojeksjoner? Gjenopprettet fra: gisgeography.com
- USGS. Kartprojeksjoner. Gjenopprettet fra: icsm.gov.au
- Weisstein, Eric W. "Albers Equal Area Conic Projection." Gjenopprettet fra: mathworld.wolfram.com
- Weisstein, Eric W. “Conic Projection” Gjenopprettet fra: mathworld.wolfram.com
- Weisstein, Eric W. “Lambert Conformal Conic Projection” Gjenopprettet fra: mathworld.wolfram.com
- Wikipedia. Liste over kartprojeksjoner. Gjenopprettet fra: en.wikipedia.com



Ingen har kommentert denne artikkelen ennå.