
Mercator projeksjonsegenskaper, bruksområder, fordeler, ulemper
De Mercator-projeksjon er et system for grafisk å representere jordoverflaten på et plan for å lage kart. Blant de nesten 400 kartografiske fremskrivningene som finnes, er Mercator en type sylindrisk projeksjon..
Gerardus Mercator, i 1569, forestilte seg jorden i en sylinder hvis diameter var lik jordens ekvator. Deretter projiserte han linjer fra midten av jorden til sylinderen. Dermed representerte den alle punktene i jordens overflatekontur, som når de sammenføyes representerer linjene til de geografiske formene.
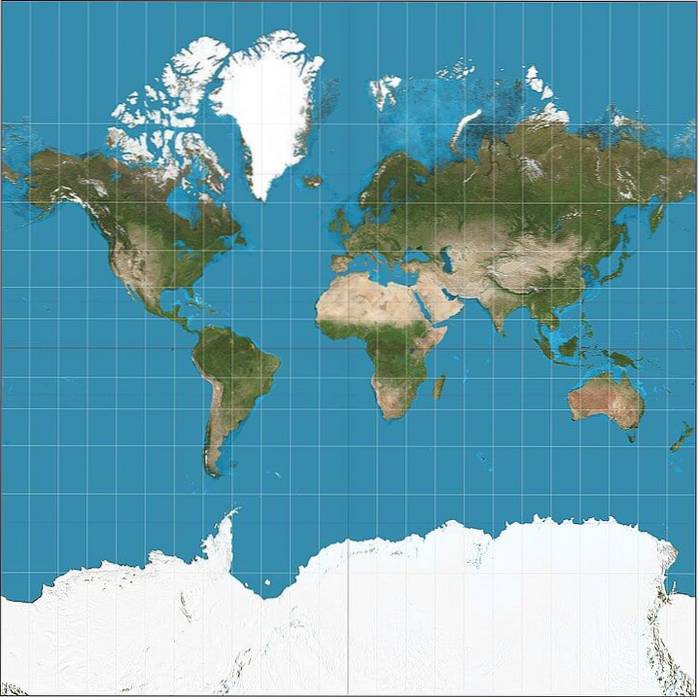
Kartene som er oppnådd med denne projeksjonen er spesielt nyttige for navigasjonskart, siden det gjør det mulig å spore ruter ved hjelp av en rett linje..
Hovedfordelen er at den representerer de geografiske formene veldig bra og holder de virkelige vinklene. Imidlertid endrer det proporsjonene av landområder når vi beveger oss bort fra ekvator..
Artikkelindeks
- 1 Kjennetegn ved Mercator-projeksjonen
- 1.1 Kartprojeksjoner
- 1.2 Sylindrisk projeksjon
- 1.3 Kartorientering
- 2 bruksområder
- 2.1 Navigering
- 2.2 Skoleformål
- 2.3 Geografiske posisjoneringssystemer på nettet
- 3 fordeler
- 4 Ulemper
- 4.1 De geografiske polene
- 5 Referanser
Kjennetegn ved Mercator-projeksjonen
Kartprojeksjoner
Jorden har en form som ligner på en sirkulerende ellips (geoid, med flate poler og en utbulende ekvator). På denne buede overflaten er konturene til kontinentene og øyene.
Dette innebærer en vanskelighetsgrad når man prøver å representere den buede overflaten i et plan, og for dette bruker geografene anslagene. Imidlertid genererer alle projeksjonene noen deformasjon eller forvrengning med hensyn til virkeligheten, og ingen metode representerer nøyaktig den virkelige jordoverflaten.
Derfor er det forskjellige typer kartografiske projeksjoner, hver med fordeler og ulemper som kan være flate, koniske, sylindriske eller polyedrale, blant andre. I dette tilfellet er Mercator-projeksjonen en sylindrisk projeksjon.
Sylindrisk projeksjon
For å løse problemet med å projisere jordoverflaten på planet, forestilte Mercator seg jorden inne i en sylinder med samme diameter. Der hoved- eller lengdeaksen til sylinderen falt sammen med jordrotasjonen (normal sylindrisk projeksjon).
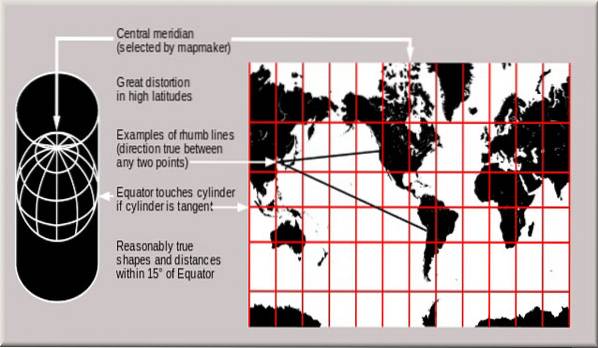
Deretter projiserte den imaginære linjer fra sentrum av planeten som passerte gjennom hvert punkt i jordens overflatekontur til den snappet opp sylinderen. Dermed projiserte han hvert punkt på kartet på sylinderen, og ved å utvide det som et plan og sammenføye punktene, fikk han et ganske nøyaktig bilde av jordens kontur.
I dette tilfellet er det en samsvarende normal sylindrisk projeksjon, hvor formene og vinklene opprettholdes. Som avstandene, men ikke de relative proporsjonene til flatene i planet.
Kartorientering
Kartet konstruert ved hjelp av Mercator-projeksjonen er også preget av å være orientert med nord oppover og med Europa som okkuperer sentrum. Selv om dette virker opplagt på grunn av den omfattende bruken som gjøres av dette kartet, er virkeligheten at like gyldige kart kan lages fra forskjellige perspektiver.
applikasjoner
Navigasjon
Denne typen kartprojeksjon ble designet av Mercator for å lage navigasjonskart (kart beregnet for bruk av sjøfolk). Siden da har den blitt brukt til dette formålet, med tanke på at det er enkelt å spore ruter med konstant kurs ved hjelp av rette linjer..
Skoleformål
På den annen side har bruken av den blitt utbredt ettersom den brukes som en reell fremstilling av jorden i andre områder. Slik finner vi det i lærebøker, på skolens veggkart og mange andre sammenhenger..
Imidlertid er det blitt påpekt at kart som er konstruert ved hjelp av Mercator-projeksjonen ikke skal brukes til skoleutdanning. Dette skyldes at forholdet mellom overflater mellom kontinenter er deformert.
Dermed opprettholder kontinentene med den største landmassen rundt ekvator en relativ overflate på kartet som ligner på den virkelige. Kontinentene som ligger nord for ekvator er imidlertid større enn ekte..
Gall-Peters-projeksjonen fra 1885, som er en like stor normal sylindrisk projeksjon, er blitt foreslått brukt til skoleformål. Det sparer overflateproporsjoner og begrenser Mercator-projeksjonen for navigasjonskart, der dens egenskaper gjør den effektiv..
Geografiske posisjoneringssystemer på WEB
Online geolokaliseringssystemer via INTERNETT, som f.eks Google Kart, bruk Mercator-projeksjonen. Spesielt den såkalte Web Mercator Projection eller Google Web Mercator, som Google vedtok i 2005, og ble utbredt blant online-kartleverandører.
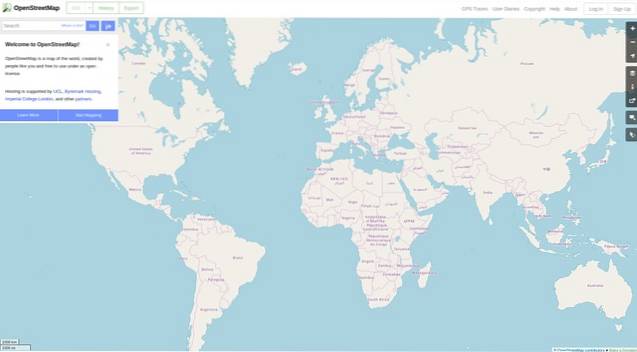
Dette skyldes hovedsakelig det faktum at de matematiske beregningene som kreves for utførelsen er enklere enn for andre typer projeksjoner. I tillegg til det faktum at i denne projiseringen holdes vinklene slik de egentlig er.
Fordel
Mercator-projeksjonskartet er ideelt for å tegne rettlinjeruter for navigering og inkluderer en geometrisk formel for å korrigere for forvrengninger ved å transformere målinger til breddegrad. På den annen side holder denne kartprojeksjonen vinklene mellom punktene slik de egentlig er..
I tillegg, som allerede antydet, har Mercator-projeksjonen den store fordelen av den lavere kompleksiteten av de matematiske operasjonene som er nødvendige for å realisere den..
Ulemper
Den grunnleggende ulempen med Mercator-projeksjonen for kart har å gjøre med proporsjonene av landmassestørrelser. I nærheten av ekvator opprettholdes proporsjonene, men når vi beveger oss bort fra ekvator øker områdene med hensyn til virkeligheten.
Dette er fordi projeksjonen ble laget på en sylinder, der bare ekvator er tangent til den, uten å kompensere for den genererte deformasjonen. Poeng på høyden av ekvator er parallelle med sylinderen, mens punkter bort fra den ikke er det..
I sistnevnte krysser linjene som projiserer dem sylinderen på diagonale punkter og lenger fra hverandre. Derfor utvides parallellene og meridianene til referansesystemet eller koordinatene mot nord og mot sør..

Dette har som konsekvens at når vi observerer et kart laget med Mercator-projeksjonen, ser vi for eksempel Alaska større enn Brasil. Imidlertid er realiteten at Brasil er 5 ganger større enn Alaska.
Akkurat som det også gir inntrykk av at den iberiske halvøya er nesten like stor som Venezuela eller Colombia, når de er større. Tilsvarende ses Russland på Mercator-kartet 7 ganger større enn Australia, når det bare har et område som er dobbelt så stort som dette kontinentet..
De geografiske polene
En annen mangel på Mercator-projeksjonen er at i det genererte kartet er både nordpolen og sørpolen utenfor området. Dette er spesielt problematisk for Sydpolen, der kontinentet Antarktis ligger..
Referanser
- Fernández-Coppel, I.A. (s (f). UTM (Universal Transversa Mercator) projeksjon. Geografiske steder. Higher Technical School of Agrarian Engineering. University of Valladolid.
- Gómez-Moreno, R.A. (2004). Kartprojeksjonsguide. Statistikk Nasjonalt institutt. Geografi og informatikk. Mexico.
- Miraglia, M., Flores, A.P., Rivarola og Benitez, M., D'Liberis, M., Galván, L., Natale, D. og Rodríguez, M. (2010). Manual of Cartography, Remote Sensing and Geographic Information Systems. Geographic Information Systems Laboratory. Instituto del Conurbano. National University of General Sarmiento.
- Raisz, E. og Mantero, J.M. (2005). Generell kartografi. Trad. 7. utgave Omega, Barcelona.
- Robinson, A.H., Sale, R.D., Morrison, J.L., Muehrcke, P.C., Ravella-Vives, J.M., Ferrer, R.M. (1987). Kartleggingselementer. Omega 1. utgave.

Ingen har kommentert denne artikkelen ennå.