Hva er partikkelenes likevekt? (Med eksempler)

De partikkelvekt Det er en tilstand der en partikkel blir funnet når de ytre kreftene som virker på dem, blir annerledes. Dette forutsetter at den opprettholder en konstant tilstand, på en slik måte at den kan forekomme på to forskjellige måter avhengig av den spesifikke situasjonen.

Den første er å være i statisk likevekt, hvor partikkelen er immobile; og det andre er den dynamiske likevekten, der summasjonen av krefter avbrytes, men likevel har partikkelen jevn rettlinjet bevegelse.

Partikkelmodellen er en veldig nyttig tilnærming for å studere kroppens bevegelse. Den består i å anta at all kroppens masse er konsentrert i et enkelt punkt, uavhengig av størrelsen på objektet. På denne måten kan du representere en planet, en bil, et elektron eller en biljardkule.

Artikkelindeks

• 1 Den resulterende kraften
• 2 frikroppsdiagrammer
• 3 måter å bruke likevektstilstanden på
  • 3.1 To krefter av samme størrelse og motsatt retning og retninger
  • 3.2 To krefter av forskjellig størrelse, samme retning og motsatt retning
  • 3.3 To krefter av samme størrelse og ulik retning
  • 3.4 Tre krefter med ulik retning
• 4 friksjon
  • 4.1 Den dynamiske friksjonen
• 5 Arbeidet eksempel
  • 5.1 Løsning
• 6 Referanser

Den resulterende kraften

Poenget som representerer objektet er hvor kreftene som påvirker det virker. Alle disse kreftene kan erstattes av en enkelt som har samme effekt, som kalles resulterende kraft eller nettokraft og er betegnet som F_R eller F_N.

I følge Newtons andre lov, når det er en ubalansert resulterende kraft, opplever kroppen en akselerasjon proporsjonal med kraften:

F_R = m.a

Hvor til er akselerasjonen som gjenstanden får takket være kraftens og m er massen til objektet. Hva skjer hvis kroppen ikke blir akselerert? Akkurat det som ble indikert i begynnelsen: kroppen er i ro eller beveger seg med jevn rettlinjet bevegelse, som mangler akselerasjon.

For en partikkel i likevekt er det gyldig å sikre at:

F_R = 0

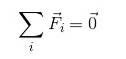
Siden tilsetning av vektorer ikke nødvendigvis innebærer å legge til modulene, må vektorene spaltes. Dermed er det gyldig å uttrykke:

F_x = m.a_x = 0; F_Y = m.a_Y = 0; F_z = m.a_z = 0

Gratis kroppsdiagrammer

For å visualisere kreftene som virker på partikkelen, er det praktisk å lage et frikroppsdiagram der alle kreftene som virker på objektet er representert av piler..

Ovennevnte ligninger er vektor i naturen. Når de bryter ned kreftene, kjennetegnes de av tegn. På denne måten er det mulig at summen av komponentene er null.

Følgende er viktige retningslinjer for å gjøre tegningen nyttig:

- Velg et referansesystem der den største mengden krefter er plassert på koordinataksene.

- Vekten trekkes alltid loddrett ned.

- Når det gjelder to eller flere overflater i kontakt, er det normale krefter som alltid trekkes ved å skyve kroppen og vinkelrett på overflaten som utøver den..

- For en partikkel i likevekt kan det være friksjoner parallelt med kontaktoverflaten og motsette seg den mulige bevegelsen, hvis partikkelen anses i hvile, eller definitivt i opposisjon, hvis partikkelen beveger seg med MRU (ensartet rettlinjet bevegelse).

- Hvis det er et tau, blir spenningen alltid trukket langs det og trekker kroppen.

Måter å anvende likevektstilstanden på

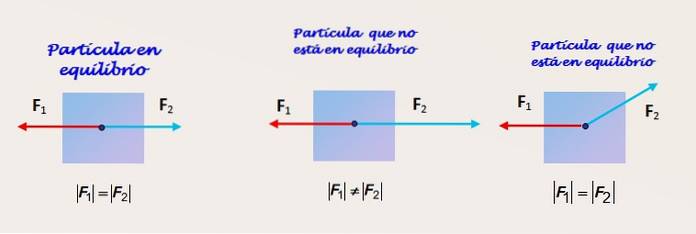
To krefter av like stor størrelse og motsatt retning og retninger

Figur 2 viser en partikkel som to krefter virker på. I figuren til venstre mottar partikkelen virkningen av to krefter F₁ og F_to som har samme styrke og virker i samme retning og i motsatt retning.

Partikkelen er i likevekt, men likevel er det ikke mulig å vite om likevekten er statisk eller dynamisk med den oppgitte informasjonen. Mer informasjon er nødvendig om den treghetsreferanserammen objektet blir observert fra.

To krefter av forskjellig størrelse, i samme retning og motsatt retning

Figuren i sentrum viser den samme partikkelen, som denne gangen ikke er i likevekt, siden størrelsen på kraften F_to er større enn F₁. Derfor er det en ubalansert kraft og objektet har en akselerasjon i samme retning som F_to.

To krefter av samme størrelse og ulik retning

Til slutt ser vi på figuren til høyre en kropp som ikke er i likevekt. Til tross for at F₁ og F_to ha like stor styrke, kraften F_to er ikke i samme retning som 1. Den vertikale komponenten av F_to motvirkes ikke av noen andre, og partikkelen opplever en akselerasjon i den retningen.

Tre krefter med ulik retning

Kan en partikkel utsatt for tre krefter være i likevekt? Ja, så lenge du plasserer enden og slutten av hver enkelt, er den resulterende figuren en trekant. I dette tilfellet er vektorsummen null.

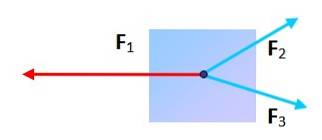
Friksjon

En kraft som ofte griper inn i partikkelenes likevekt er statisk friksjon. Det skyldes samspillet mellom objektet representert av partikkelen og overflaten til en annen. For eksempel er en bok i statisk likevekt på et skrått bord modellert som en partikkel og har et frikroppsdiagram som følgende:

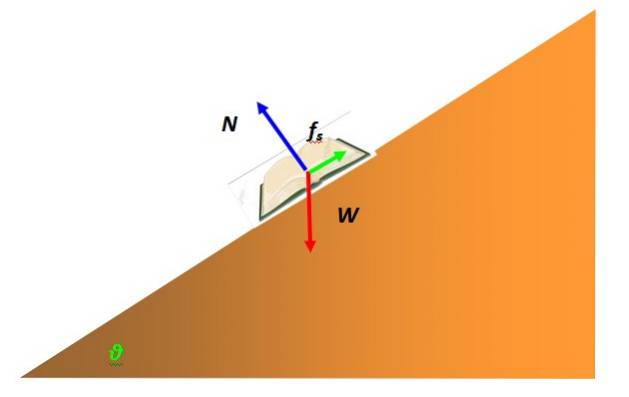
Kraften som forhindrer at boken glir over overflaten av det skråplanet og forblir i ro, er statisk friksjon. Det avhenger av naturen til overflatene i kontakt, som mikroskopisk presenterer ruhet med topper som griper sammen hverandre, noe som gjør bevegelse vanskelig..

Den maksimale verdien av statisk friksjon er proporsjonal med den normale kraften, kraften som utøves av overflaten på det støttede objektet, men vinkelrett på overflaten. I eksemplet i boka er det angitt i blått. Matematisk uttrykkes det slik:

F_{s mer}∝ N

Konstanten av proporsjonalitet er statisk friksjonskoeffisient μ_s, som er bestemt eksperimentelt, er dimensjonsløs og avhenger av arten av overflatene i kontakt.

F_{s maks} = μ_s N

Den dynamiske friksjonen

Hvis en partikkel er i dynamisk likevekt, finner bevegelse allerede sted og statisk friksjon griper ikke lenger inn. Hvis det er noen friksjonskraft som motarbeider bevegelsen, virker den dynamiske friksjonen, hvis størrelse er konstant og er gitt av:

F_k = μ_k N

Hvor μ_k er han dynamisk friksjonskoeffisient, Det avhenger også av typen overflater i kontakt. I likhet med den statiske friksjonskoeffisienten er den dimensjonsløs og verdien bestemmes eksperimentelt.

Verdien av koeffisienten for dynamisk friksjon er vanligvis mindre enn den for statisk friksjon.

Arbeidet eksempel

Boken i figur 3 er i ro og har en masse på 1,30 kg. Flyet har en hellingsvinkel på 30º. Finn koeffisienten for statisk friksjon mellom boka og plan overflate.

Løsning

Det er viktig å velge et passende referansesystem, se følgende figur:

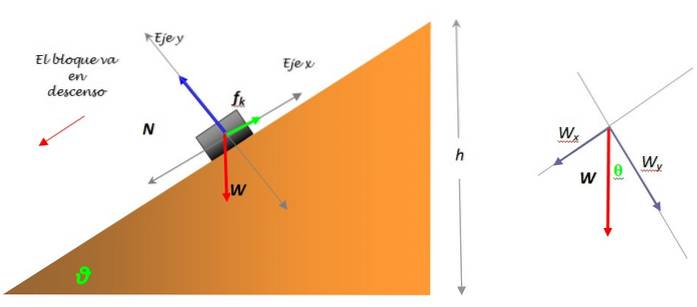
Vekten av boken har styrke W = mg, det er imidlertid nødvendig å dele den opp i to komponenter: W_x Y W_Y, siden det er den eneste kraften som ikke faller rett over noen av koordinataksene. Nedbrytningen av vekten observeres i figuren til venstre.

W_Y = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N

W_x = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N

Den andre. Newtons lov for den vertikale aksen er:

N - Wy = 0

N = mg. cos θ = 11,03 N.

Bruk av 2.. Newtons lov for x-aksen, og valgte retningen til den mulige bevegelsen som positiv:

W_x - F_s = 0

Maksimal friksjon er F_{s maks}= μ_sN, Og dermed:

W_x - μ_sN = 0

μ_s = W_x / N = 6,37 / 11,03 = 0,58

Referanser

1. Rex, A. 2011. Fundamentals of Physics. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7^ma. Ed. Cengage Learning. 120 - 124.
3. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 99-112.
4. Tippens, P. 2011. Fysikk: Konsepter og applikasjoner. 7. utgave. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fysikk. Addison Wesley. 148-164.