Hva er coplanar vektorer? (Med øvelser løst)

De coplanar vektorer eller koplanar er de som er inneholdt i samme plan. Når det bare er to vektorer, er de alltid i samme plan, siden det er uendelige plan, er det alltid mulig å velge en som inneholder dem.

Hvis du har tre eller flere vektorer, kan det hende at noen av dem ikke er i samme plan som de andre, derfor kan de ikke betraktes som plan. Følgende figur viser et sett med koplanære vektorer angitt med fet skrift TIL, B, C Y D:

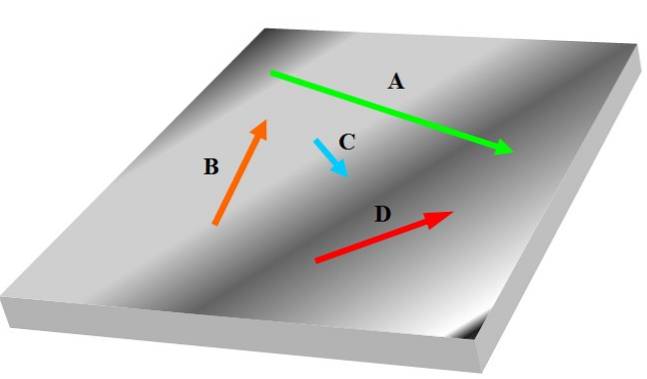
Vektorer er relatert til oppførselen og egenskapene til relevante fysiske størrelser innen vitenskap og teknologi; for eksempel hastighet, akselerasjon og kraft.

En kraft gir forskjellige effekter på et objekt når måten det påføres på varieres, for eksempel ved å endre intensitet, retning og retning. Selv om du bare endrer en av disse parameterne, er resultatene betydelig forskjellige..

I mange applikasjoner, både i statikk og dynamikk, er kreftene som virker på en kropp på samme plan, derfor betraktes de som plan.

Artikkelindeks

• 1 Betingelser for at vektorene skal være i samme plan
  • 1.1 Blandet produkt mellom tre vektorer
• 2 Søknader
  • 2.1 Coplanar, samtidige og ikke-kollinære krefter
• 3 Løst øvelser
  • 3.1-Øvelse 1
  • 3.2-Øvelse 2
• 4 Referanser

Betingelser for at vektorene skal være i samme plan

For at tre vektorer skal være i samme plan, må de ligge på samme plan, og dette skjer hvis de oppfyller noen av følgende betingelser:

-Vektorer er parallelle, derfor er komponentene proporsjonale og lineært avhengige.

-Det blandede produktet ditt er null.

-Hvis du har tre vektorer og noen av dem kan skrives som en lineær kombinasjon av de to andre, er disse vektorene koplanare. For eksempel, en vektor som kommer fra summen av to andre, de tre er alle i samme plan.

Alternativt kan koplanaritetsbetingelsen fastsettes som følger:

U V w er koplanar hvis det er tre (skalar) tall α, β, γ slik at αeller + βv + γw = 0 med (α, β, γ) annet enn (0, 0, 0)

Blandet produkt mellom tre vektorer

Det blandede produkt mellom vektorene er definert av tre vektorer eller, v Y w, resulterer i en skalar som er resultatet av å utføre følgende operasjon:

eller · (v x w) = eller · (v x w)

For det første utføres kryssproduktet som er i parentes: v x w, hvis resultat er en normal vektor (vinkelrett) på planet hvor begge v Hva w.

Ja eller er på samme plan som v Y w, naturlig skal skalarproduktet (punktprodukt) mellom u og nevnte normale vektor være 0. På denne måten bekreftes det at de tre vektorene er koplanare (de ligger på samme plan).

Når det blandede produktet ikke er null, er resultatet lik volumet av parallelepiped som har vektorene eller, v Y w som tilstøtende sider.

applikasjoner

Coplanar, samtidige og ikke-kollinære styrker

Styrkene samtidig de brukes alle til samme punkt. Hvis de også er i samme plan, kan de erstattes av en enkelt, som kalles resulterende kraft og har samme effekt som de opprinnelige kreftene.

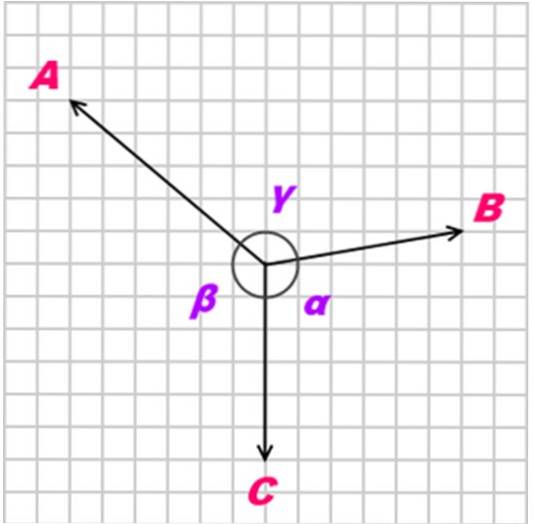
Hvis en kropp er i likevekt takket være tre koplanære krefter, samtidig og ikke kollinær (ikke parallell), kalt TIL, B Y C, de Lamys teorem påpeker at forholdet mellom disse kreftene (størrelser) er som følger:

A / sin α = B / sin β = C / sin γ

Med α, β og γ som motsatte vinkler til de påførte kreftene, som vist i følgende figur:

Løst øvelser

-Øvelse 1

Finn verdien av k slik at følgende vektorer er i samme plan:

eller = <-3, k, 2>

v = <4, 1, 0>

w = <-1, 2, -1>

Løsning

Siden vi har komponentene i vektorene, brukes kriteriet for det blandede produktet, derfor:

eller · (v x w) = 0

Det løses først v x w. Vektorene vil bli uttrykt i form av enhetsvektorene Jeg, j Y k som skiller de tre vinkelrette retningene i rommet (bredde, høyde og dybde):

v= 4 Jeg + j + 0 k

w= -1 Jeg + toj -1 k

v x w = -4 (i x i) + 8 (i x j) - 4 (i x k) - (j x i) + to (j x j) - to (j x k) = 8 k + 4 j + k -to jeg = -to Jeg + 4 j + 9 k

Nå vurderer vi det skalære produktet mellom u og vektoren som er resultatet av forrige operasjon, og setter operasjonen lik 0:

eller (v x w) = (-3 Jeg + k j + to k) · (-to Jeg + 4 j + 9 k) = 6 + 4k +18 = 0

24 + 4k = 0

Den etterspurte verdien er: k = - 6

Så vektoren eller Det er:

eller = <-3, -6, 2>

-Trening to

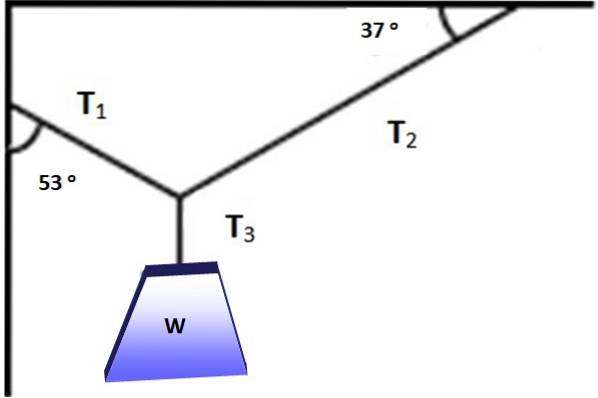
Figuren viser et objekt med en vekt på W = 600 N, som henger i likevekt takket være kablene plassert i vinklene vist på figur 3. Er det mulig å anvende Lamys setning i denne situasjonen? I alle fall finne størrelsen på T₁, T_to Y T₃ som gjør balanse mulig.

Løsning

Lamys teorem er anvendelig i denne situasjonen hvis noden som de tre spenningene påføres blir vurdert, siden de utgjør et system av koplanære krefter. Først lages frikroppsdiagrammet for hengende vekt for å bestemme størrelsen på T_3:

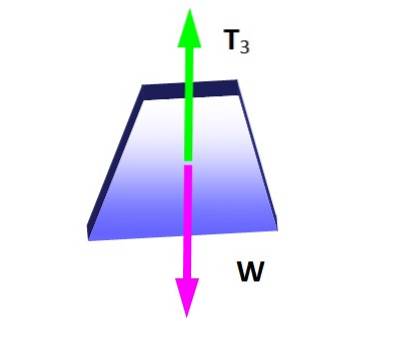
Fra likevektstilstanden følger det at:

T₃  = W = 600 N

Vinklene mellom kreftene er markert med rødt i følgende figur, det kan enkelt verifiseres at summen er 360º. Nå er det mulig å bruke Lamys teorem, siden en av kreftene og de tre vinklene mellom dem er kjent:

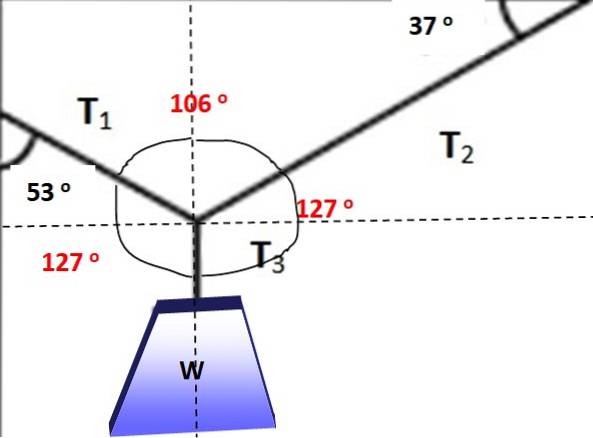
T₁ / sin 127º = W / sin 106º

Derfor: T₁ = sin 127º (W / sin 106º) = 498,5 N

Igjen brukes Lamys teorem for å løse T_to:

T_to / sin 127 = T₁ / sin 127º

T_to = T₁ = 498,5 N

Referanser

1. Figueroa, D. Series: Physics for Sciences and Engineering. Volum 1. Kinematikk. 31-68.
2. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: frtl.utn.edu.ar
3. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Publishing Company 28-66.
4. McLean, W. Schaum-serien. Mekanikk for ingeniører: Statikk og dynamikk. 3. utgave. McGraw Hill. 1-15.
5. Wikipedia. Vector. Gjenopprettet fra: es.wikipedia.org.