
Trigonometriske forhold eksempler, øvelser og applikasjoner
De trigonometriske forhold er kvotienter eller forhold som kan gjøres med verdien av sidene til en rett trekant. Disse sidene er: to ben som danner 90º med hverandre og hypotenusen, som danner den spisse vinkelen θ med det ene benet.
Du kan danne 6 kvoter. Deres navn og respektive forkortelser er:
- bryst (sen)
- cosinus (cos)
- tangens (tg eller tan)
- cotangent (ctg eller cotan)
- secant (sek) og
- cosecant (cosec)
Alle refererte til vinkel θ, som vist i følgende figur:
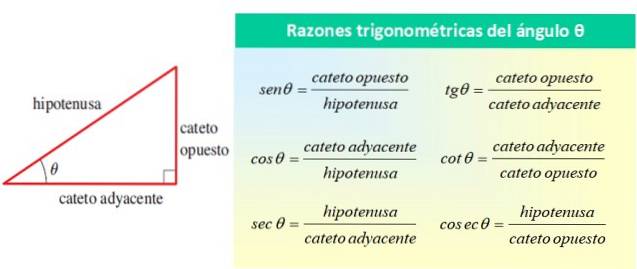
De grunnleggende trigonometriske forholdene til vinkelen θ er sin θ, cos θ og tan θ, mens de gjenværende forholdene kan uttrykkes i termer av disse tre. Fra tabellen ovenfor kan det sees at:
- sek θ = 1 / cos θ
- cosec θ = 1 / sin θ
- barneseng θ = 1 / tg θ
Størrelsen på sidene av trekanten påvirker ikke verdien av forholdene, siden to trekanter hvis vinkler måler det samme er like trekanter og de respektive forholdene mellom sidene har samme verdi.
Artikkelindeks
- 1 Eksempel
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Anvendelser av trigonometriske forhold
- 4 Referanser
Eksempel
La oss for eksempel beregne de trigonometriske forholdene til vinkelen θ i følgende trekanter:
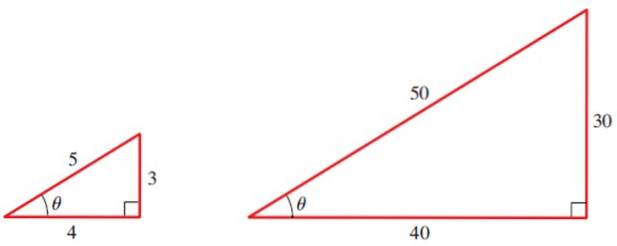
For den lille trekanten har vi de tre grunnleggende forholdene til vinkelen θ:
sin θ = 3/5
cos θ = 4/5
tg θ = ¾
La oss nå beregne de tre grunnleggende forholdene of med den store trekanten:
sin θ = 30/50 = 3/5
cos θ = 40/50 = 4/5
tg θ = 30/40 = ¾
En viktig detalj å ta hensyn til er følgende: både sin θ og cos θ er mindre enn 1, siden bena alltid måler mindre enn hypotenusen. Faktisk:
sin θ = 3/5 = 0,6
cos θ = 4/5 = 0,8
Løst øvelser
I de følgende øvelsene blir du bedt om å løse den rette trekanten, som betyr å finne lengden på de tre sidene og målene på de indre vinklene, hvorav den ene alltid måler 90º.
Pythagoras teorem gjelder rette trekanter og er veldig nyttig når to av sidene er kjent og den manglende siden må bestemmes. Teoremet går slik:
Hypotenuseto = motsatt bento + tilstøtende bento
Vi kan sjekke pythagorasetningen med den lille trekanten i figur 2, hvis ben er 3 og 4. Rekkefølgen som bena tas i, spiller ingen rolle. Vi bruker setningen vi har:
Hypotenuseto = 3to + 4to = 9 + 16 = 25
Derfor er hypotenusen:
Hypotenuse = √25 = 5
- Øvelse 1
Beregn trigonometriske forhold for vinklene vist i følgende trekanter:

Løsning til
Denne trekanten er den samme som i figur 3, men vi blir bedt om de trigonometriske forholdene til den andre spisse vinkelen, betegnet α. Uttalelsen tilbyr ikke verdien av hypotenusen, men ved å anvende den pythagoriske teorien vet vi at den er verdt 5.
Forholdene kan beregnes direkte fra definisjonen, og ta vare når du velger benet som er det motsatte av vinkelen α å beregne sin α. La oss se:
- sin α = 4/5
- cos α = 3/5
- tg α = 4/3
- barneseng α = ¾
- sek α = 1 / (3/5) = 5/3
- cosec α = 1 / (4/5) = 5/4
Og som vi kan se, er verdiene til de trigonometriske forholdene byttet ut. Faktisk er α og θ komplementære vinkler, noe som betyr at de legger opp til 90º. I dette tilfellet er det sant at sin α = cos θ og så videre av andre grunner.
Løsning b
La oss beregne hypotenusen til trekanten ved hjelp av Pythagoras teorem:
Hypotenuseto = 20to + tjueento = 841
√841 = 29
Da er de 6 trigonometriske forholdene til vinkelen β:
- sin β = 20/29
- cos β = 21/29
- tg β = 20/21
- barneseng β = 21/20
- sek β = 1 / (21/29) = 29/21
- cosec β = 1 / (20/29) = 20/29
- Øvelse 2
a) Finn verdien av x i figuren.
b) Beregn omkretsen til de tre viste trekanter.
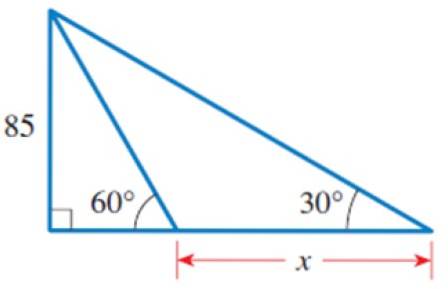
Løsning til
I figuren kan vi identifisere flere trekanter, spesielt høyre trekant til venstre, som har et ben lik 85 og den spisse vinkelen 60º.
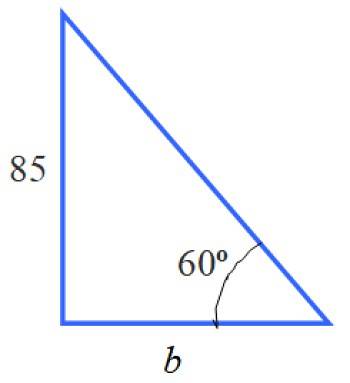
Med informasjonen fra denne trekanten kan vi beregne side b. Det er ikke tiltaket som uttalelsen krever, men å vite verdien er et tidligere trinn.
For å bestemme dette er det passende forholdet tg 60º = 85 / b, siden b er benet ved siden av 60 ° og 85 er det motsatte av nevnte vinkel. Derfor:
b = 85 / tg 60º = 85 / √3
Når b er kjent, vil vi bruke den store og ytre høyre trekanten, som har en felles side med den forrige trekanten: den som måler 85. Dette er benet motsatt 30 ° vinkelen..
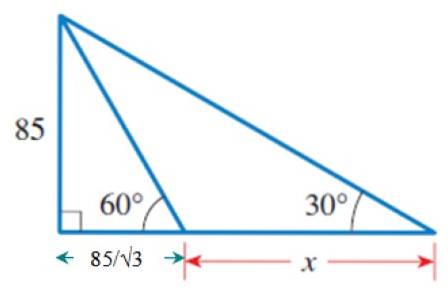
Derfra:
Ben ved siden av 30º = (85 / √3) + x
Nå kan vi foreslå følgende:
85 / [(85 / √3) + x] = tg 30º
Det som er i parentes multipliserer tilfeldigvis tg 30º:
85 = [(85 / √3) + x]. tg 30º
Bruk av fordelingsegenskapen til multiplikasjon:
85 = tg 30 °. (85 / √3) + x. tg 30º
Derfor:
x.tg 30º = 85 - tg 30º. (85 / √3) = 85 [1 - tg 30º. (1 / √3)] = 85. (2/3) = 170/3
Erstatter verdien tg 30º = √3 / 3:
x = (170/3) ÷ (√3 / 3) = 98,15
Løsning b
Omkrets av den lille trekanten
La h1 hypotenusen til denne trekanten, som kan beregnes ved hjelp av Pythagoras teorem eller ved hjelp av et trigonometrisk forhold, for eksempel cos 60º:
cos 60 º = 85 / √3 / t1→ h1 = (85 / √3) ÷ cos 60º = 98.1
For å finne P, omkretsen av denne trekanten, legger vi ganske enkelt til de tre sidene:
P = 85 + (85 / √3) + 98,1 = 232,2
Omkrets av den ytre trekanten
La hto til hypotenusen til den ytre trekanten:
sin 30º = 85 ÷ hto
hto = 85 ÷ sin 30º = 170
For denne trekanten er omkretsen:
P = 85 + [(85 / √3) + 98,15] + 170 = 402,22
Omkrets av ikke-høyre trekant
Vi kjenner allerede alle sidene av denne trekanten:
P = x + h1 + hto = 98,15 + 98,15 + 170 = 366,3
Anvendelser av trigonometriske forhold
Trigonometriske forhold har mange praktiske anvendelser, for eksempel kan høyder beregnes.
Anta at et vanntårn ligger 100 meter fra en bygning. En observatør ved et vindu merker at stigningsvinkelen til den øvre enden av tårnet er 39 º, mens depresjonsvinkelen som tårnets bunn blir sett på er 25 º. Han lurer på:
a) Hva er høyden på tårnet?
b) Hvor høyt vinduet er?
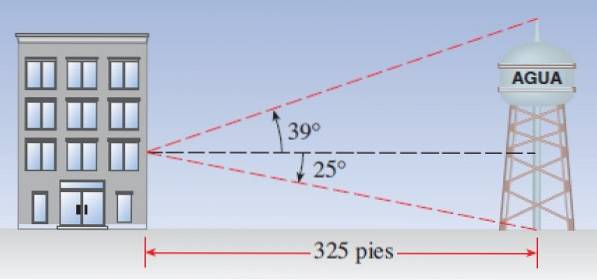
Løsning til
Fra benet motsatt 39º av den øvre trekanten får vi en del av svaret:
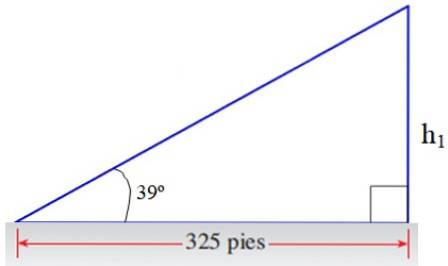
h1/ 325 = tg 39º → h1 = 325. tg 39º fot = 263,2 fot
På en lignende måte får vi resten av høyden på tårnet, kalt hto startende fra den nedre trekanten:
hto/ 325 = tg 25º → hto = 325. tg 25º fot = 151,6 fot
Den totale høyden på tårnet er h1 + hto = 263,2 + 151,6 fot = 414,7 fot.
Løsning b
Vinduet er nettopp i en høyde hto bakke:
hto = 151,6 fot.
Referanser
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Hoffman, J. Selection of Mathematics Topics. Volum 3.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Utgave. Cengage læring.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.



Ingen har kommentert denne artikkelen ennå.