
Eksponensiell utjevningsmetode og eksempel
De eksponensiell utjevning det er en måte å forutsi etterspørselen etter en vare for en gitt periode. Denne metoden anslår at etterspørselen vil være lik gjennomsnittet av det historiske forbruket i en gitt periode, noe som gir verdiene som er nærmere i tid større vekt eller vekt. I tillegg, for følgende prognoser ta hensyn til den eksisterende feilen i den nåværende prognosen.
Forespørsel om etterspørsel er metoden for å projisere kundenes etterspørsel etter et produkt eller en tjeneste. Denne prosessen er kontinuerlig, der ledere bruker historiske data for å beregne hva de forventer at salgets etterspørsel etter en vare eller tjeneste skal være..
Informasjon fra selskapets fortid brukes ved å legge den til de økonomiske dataene i markedet for å se om salget vil øke eller redusere.
Resultatene av etterspørselsprognosen brukes til å sette mål for salgsavdelingen, og prøve å holde seg i tråd med selskapets mål.
Artikkelindeks
- 1 Eksponensiell utjevningsmetode
- 1.1 Utjevning i prognosen
- 1.2 Vektet glidende gjennomsnitt
- 1.3 Eksponensiell utjevning
- 2 Eksempel
- 3 Referanser
Eksponensiell utjevningsmetode
Utjevning er en veldig vanlig statistisk prosess. Utjevnede data finnes ofte i ulike former for hverdag. Hver gang et gjennomsnitt brukes til å beskrive noe, brukes et utjevnet tall.
Anta at den varmeste vinteren på rekorden ble opplevd i år. For å kvantifisere det starter vi med settet med daglige temperaturdata for vinterperioden i hvert registrerte historiske år..
Dette genererer et antall tall med store "hopp". Du trenger et tall som eliminerer alle disse hoppene fra dataene for å lettere kunne sammenligne en vinter med en annen.
Å eliminere hoppet i dataene kalles utjevning. I dette tilfellet kan et enkelt gjennomsnitt brukes for å oppnå utjevning.
Utjevning i prognosen
For å forutsi etterspørsel brukes utjevning også for å eliminere variasjoner i historisk etterspørsel. Dette muliggjør bedre identifisering av etterspørselsmønstre, som kan brukes til å estimere fremtidig etterspørsel..
Variasjoner i etterspørsel er det samme konseptet som "hopp" av temperaturdata. Den vanligste måten at variasjoner i etterspørselshistorikken fjernes, er å bruke et gjennomsnitt, eller spesifikt, et glidende gjennomsnitt..
Det glidende gjennomsnittet bruker et forhåndsdefinert antall perioder for å beregne gjennomsnittet, og disse periodene beveger seg etter hvert som tiden går..
For eksempel, hvis et fire måneders glidende gjennomsnitt brukes og i dag er 1. mai, vil den gjennomsnittlige etterspørselen for januar, februar, mars og april bli brukt. 1. juni vil kravet til februar, mars, april og mai bli brukt.
Vektet glidende gjennomsnitt
Når du bruker et enkelt gjennomsnitt, blir samme betydning lagt til hver verdi i datasettet. Derfor representerer hver måned 25% av det glidende gjennomsnittet i et glidende gjennomsnitt på fire måneder..
Ved å bruke etterspørselshistorikk til å projisere fremtidig etterspørsel, er det naturlig at den siste perioden har større innvirkning på prognosen..
Du kan tilpasse beregningen av det glidende gjennomsnittet for å bruke forskjellige "vekter" til hver periode, for å oppnå de ønskede resultatene..
Disse vektene uttrykkes i prosent. Summen av alle vekter i alle perioder må være opptil 100%.
Derfor, hvis du vil bruke 35% som vekt for den nærmeste perioden i det fire måneders vektede gjennomsnittet, kan du trekke 35% fra 100%, slik at 65% blir igjen å dele mellom de tre gjenværende periodene.
For eksempel kan du ende opp med en vekting på henholdsvis 15%, 20%, 30% og 35% for de fire månedene (15 + 20 + 30 + 35 = 100).
Eksponensiell utjevning
Kontrollinngangen for den eksponensielle utjevningsberegningen er kjent som utjevningsfaktoren. Representerer vekten som brukes på etterspørselen for den siste perioden.
Hvis 35% brukes som den siste periodevekten i beregnet vektet glidende gjennomsnitt, kan du også velge å bruke 35% som utjevningsfaktor i den eksponentielle utjevningsberegningen..
Eksponentiell del
Forskjellen i den eksponentielle utjevningsberegningen er at i stedet for å måtte finne ut hvor mye vekt som skal påføres for hver forrige periode, brukes utjevningsfaktoren til å gjøre det automatisk..
Dette er den "eksponentielle" delen. Hvis 35% brukes som utjevningsfaktor, vil etterspørselsvekten for den siste perioden være 35%. Vekten av etterspørselen fra forrige periode til den siste vil være 65% av 35%.
65% kommer fra å trekke 35% fra 100%. Dette tilsvarer en vekting på 22,75% for den perioden. Den neste siste etterspørselen vil være 65% fra 65% fra 35%, som tilsvarer 14,79%.
Den forrige perioden vil vektes som 65% av 65% av 65% av 35%, tilsvarende 9,61%. Dette vil gjøres for alle tidligere perioder, opp til den første perioden.
Formel
Formelen for beregning av eksponensiell utjevning er som følger: (D * S) + (P * (1-S)), hvor,
D = siste etterspørsel i perioden.
S = utjevningsfaktor, representert i desimalform (35% vil være 0,35).
P = prognose for den siste perioden, resultat av utjevningsberegningen for forrige periode.
Forutsatt at vi har en utjevningsfaktor på 0,35, vil vi da ha: (D * 0,35) + (P * 0,65).
Som du ser er de eneste datainngangene som kreves etterspørselen og den siste prognosen..
Eksempel
Et forsikringsselskap har besluttet å utvide markedet til den største byen i landet, og tilby forsikring for kjøretøy.
Som en første handling vil selskapet forutsi hvor mye bilforsikring som blir kjøpt av innbyggerne i denne byen.
For å gjøre dette vil de bruke som første data mengden bilforsikring kjøpt i en annen mindre by.
Forespørsel om etterspørsel for periode 1 er 2.869 kontraktsforsikring, men den faktiske etterspørselen i den perioden var 3200.
Etter selskapets skjønn tildeler det en utjevningsfaktor på 0,35. Prognosen for etterspørsel for følgende periode er: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Den samme beregningen ble gjort for hele året, med følgende sammenligningstabell mellom det som faktisk ble oppnådd og det som ble prognostisert for den måneden.
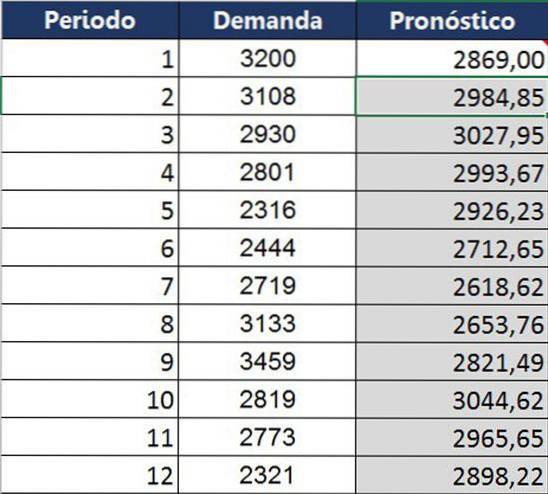
Sammenlignet med gjennomsnittsteknikker kan eksponentiell utjevning forutsi trenden bedre. Imidlertid kommer det fortsatt til kort, som vist i grafen:
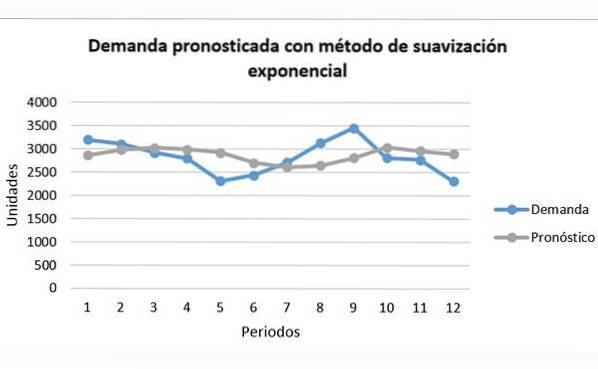
Det kan sees hvordan den grå linjen i prognosen kan være godt under eller over den blå etterspørselen, uten å kunne følge den helt.
Referanser
- Wikipedia (2019). Eksponensiell utjevning. Hentet fra: es.wikipedia.org.
- Ingenio Empresa (2016). Hvordan bruke enkel eksponentiell utjevning for å forutsi etterspørsel. Hentet fra: ingenioempresa.com.
- Dave Piasecki (2019). Eksponensiell utjevning forklart. Hentet fra: inventoryops.com.
- Studie (2019). Etterspørselsteknikker: glidende gjennomsnitt og eksponentiell utjevning. Hentet fra: study.com.
- Cityu (2019). Eksponensielle utjevningsmetoder. Hentet fra: personal.cb.cityu.edu.hk.



Ingen har kommentert denne artikkelen ennå.