De kvadratiske sekvenser, i matematiske termer består de av tallsekvenser som følger en viss regningsregel. Det er interessant å kjenne denne regelen for å bestemme noen av vilkårene i en sekvens.
En måte å oppnå dette på er å bestemme forskjellen mellom to påfølgende ord og se om verdien som oppnås alltid blir gjentatt. Når dette er tilfelle, sies det å være et vanlig suksess.
Men hvis det ikke gjentas, kan du prøve å undersøke forskjell mellom forskjeller og se om denne verdien er konstant. I så fall er det en kvadratisk sekvens.
Artikkelindeks
Følgende eksempler hjelper til med å avklare hva som er forklart så langt:
La sekvensen S = 4, 7, 10, 13, 16,…
Denne sekvensen, betegnet med S, er et uendelig tallsett, i dette tilfellet av heltall.
Det kan sees at det er en vanlig sekvens, fordi hver term oppnås ved å legge 3 til forrige term eller element:
4
4 +3 = 7
7+3 = 10
10+3 = 13
1. 3+3 = 16
Med andre ord: denne sekvensen er vanlig fordi forskjellen mellom neste periode og den forrige gir en fast verdi. I det gitte eksemplet er denne verdien 3.
De vanlige sekvensene som oppnås ved å legge til en fast mengde til forrige periode kalles også aritmetiske progresjoner. Og forskjellen -konstant- mellom påfølgende ord kalles grunnen til og er betegnet som R.
Se nå følgende sekvens:
S = 2, 6, 12, 20, 30,….
Når suksessive forskjeller beregnes, oppnås følgende verdier:
6-2 = 4
12-6 = 6
20-12 = 8
30-20 = 10
Forskjellene er ikke konstante, så det kan sies at det er en IKKE vanlig sekvens.
Imidlertid, hvis vi vurderer settet med forskjeller, har vi en annen sekvens, som vil bli betegnet som Sforskjell:
Sforskjell = 4, 6, 8, 10,….
Denne nye arven er en vanlig suksess, siden hver periode oppnås ved å legge den faste verdien R = 2 til den forrige. Derfor kan vi bekrefte at S er kvadratisk sekvens.
Det er en generell formel for å konstruere en kvadratisk sekvens:
Tn = A ∙ nto + B ∙ n + C
I denne formelen, Tn er begrepet posisjon n i sekvensen. A, B og C er faste verdier, mens n varierer en etter en, det vil si 1, 2, 3, 4, ...
I sekvensen S i forrige eksempel A = 1, B = 1 og C = 0. Derfra følger det at formelen som genererer alle ordene er: Tn = nto + n
Nemlig:
T1 = 1to + 1 = 2
Tto = 2to + 2 = 6
T3 = 3to + 3 = 12
T5 = 5to + 5 = 30
Tn = nto + n
Tn + 1 - Tn = [A ∙ (n + 1)to + B ∙ (n + 1) + C] - [A ∙ nto + B ∙ n + C]
Å utvikle uttrykket gjennom bemerkelsesverdige produkter gjenstår:
Tn + 1 - Tn = A ∙ nto + A ∙ 2 ∙ n + A + B ∙ n + B + C - A ∙ nto - B ∙ n - C
Ved å forenkle det får du:
Tn + 1 - Tn = 2 ∙ A ∙ n + A + B
Dette er formelen som gir sekvensen av forskjellene SDif som kan skrives slik:
Difn = A ∙ (2n + 1) + B
Der neste periode er tydelig 2 ∙ Noen ganger den forrige. Det vil si forholdet mellom sekvensen av forskjeller Sforskjell er: R = 2 ∙ A.
La sekvensen S = 1, 3, 7, 13, 21, .... Bestem om:
i) Er det vanlig eller ikke
ii) Er det kvadratisk eller ikke
iii) Det var kvadratisk, forskjellenes rekkefølge og forholdet mellom dem
i) La oss beregne forskjellen mellom følgende og forrige vilkår:
3-1 = 2
7-3 = 4
13-7 = 6
21-13 = 8
Vi kan bekrefte det sekvensen S er ikke vanlig, fordi forskjellen mellom suksessive begreper ikke er konstant.
ii) Sekvensen av forskjeller er regelmessig, fordi forskjellen mellom dens vilkår er den konstante verdien 2. Derfor den originale sekvensen S er kvadratisk.
iii) Vi har allerede bestemt at S er kvadratisk, forskjellenes rekkefølge er:
Sforskjell = 2, 4, 6, 8, ... og forholdet er R = 2.
La sekvensen S = 1, 3, 7, 13, 21, ... fra forrige eksempel, hvor det ble bekreftet at den er kvadratisk. Fastslå:
i) Formelen som bestemmer det generelle begrepet Tn .
ii) Sjekk tredje og femte termin.
iii) Verdien av det tiende begrepet.
i) Den generelle formelen for Tn er A ∙ nto + B ∙ n + C. Så gjenstår det å kjenne til verdiene til A, B og C.
Forskjellesekvensen har forhold 2. Videre er forholdet R for enhver kvadratisk sekvens 2 ∙ A som vist i forrige avsnitt.
R = 2 ∙ A = 2 som får oss til å konkludere med at A = 1.
Den første termen av sekvensen av forskjeller SDif er 2 og må tilfredsstille A ∙ (2n + 1) + B, med n = 1 og A = 1, det vil si:
2 = 1 ∙ (2 ∙ 1 + 1) + B
løse for B, får vi: B = -1
Da er den første termen av S (n = 1) verdt 1, det vil si: 1 = A ∙ 1to + B ∙ 1 + C. Som vi allerede vet at A = 1 og B = -1, erstatter vi:
1 = 1 ∙ 1to + (-1) ∙ 1 + C
Løsning for C får vi verdien: C = 1.
Oppsummert:
A = 1, B = -1 og C = 1
Da blir den 9. termin Tn = nto - n + 1
ii) Det tredje begrepet T3 = 3to - 3 + 1 = 7 og det er bekreftet. Den femte T5 = 5to - 5 + 1 = 21 som også er bekreftet.
iii) Den tiende periode vil være T10 = 10to - 10 + 1 = 91.
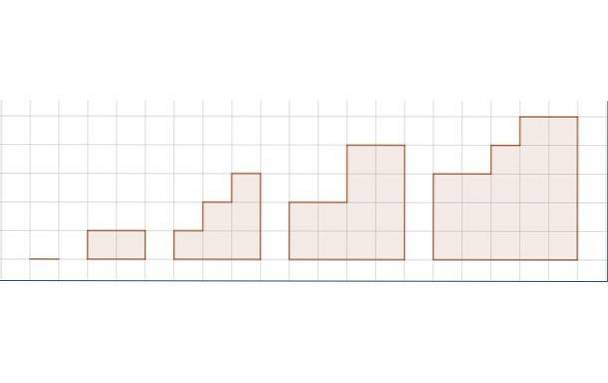
Figuren viser en sekvens på fem figurer. Gitteret representerer lengdeenheten.
i) Bestem sekvensen for området til figurene.
ii) Vis at det er en kvadratisk sekvens.
iii) Finn området i figur 10 (ikke vist).
i) Sekvensen S som tilsvarer området til figurrekkefølgen er:
S = 0, 2, 6, 12, 20,…
ii) Sekvensen som tilsvarer de påfølgende forskjellene i vilkårene i S er:
Sforskjell = 2, 4, 6, 8,…
Siden forskjellen mellom påfølgende ord ikke er konstant, er S ikke en vanlig sekvens. Det gjenstår å være kjent om det er kvadratisk, som vi igjen gjør sekvensen av forskjellene for å oppnå:
2, 2, 2,….
Siden alle vilkårene i sekvensen gjentas, er det bekreftet at S er en kvadratisk sekvens.
iii) Sekvensen Sforskjell er vanlig og forholdet R er 2. Ved å bruke ligningen vist over R = 2 ∙ A, forblir den:
2 = 2 ∙ A, noe som betyr at A = 1.
Den andre termen for sekvensen av forskjeller SDif er 4 og den niende sikt av SDif Det er
A ∙ (2n + 1) + B.
Den andre termen har n = 2. I tillegg er det allerede bestemt at A = 1, så ved å bruke den forrige ligningen og erstatte, har vi:
4 = 1 ∙ (2 ∙ 2 + 1) + B
Løsning for B får vi: B = -1.
Det er kjent at den andre termen av S er verdt 2, og at den må oppfylle formelen for den generelle termen med n = 2:
Tn = A ∙ nto + B * n + C; n = 2; A = 1; B = -1; Tto = 2
Nemlig
2 = 1 ∙ 2to - 1 ∙ 2 + C
Det konkluderes med at C = 0, det vil si at formelen som gir den generelle termen for sekvensen S er:
Tn = 1 ∙ nto - 1 ∙ n +0 = nto - n
Nå er femte periode bekreftet:
T5 = 5to - 5 = 20
iii) Figur # 10, som ikke er tegnet her, vil ha området som tilsvarer den tiende termen for sekvensen S:
T10 = 10to - 10 = 90
Ingen har kommentert denne artikkelen ennå.