Riemann sumhistorie, formler og egenskaper, øvelser

De Riemann sum er navnet på den omtrentlige beregningen av en bestemt integral, ved hjelp av en diskret summering med et begrenset antall ord. En vanlig applikasjon er tilnærmingen av funksjonsområdet på en graf.

Det var den tyske matematikeren Georg Friedrich Bernhard Riemann (1826-1866) som først tilbød en grundig definisjon av integriteten til en funksjon i et gitt intervall. Han gjorde det kjent i en artikkel publisert i 1854. 

Riemann-summen er definert på en funksjon y = f (x), med x som tilhører det lukkede intervallet [a, b]. I dette intervallet lages en partisjon P av n-elementer:

P = x₀= a, x₁, x_to,..., x_n= b

Dette betyr at intervallet er delt slik:

x_k-1 ≤ t_k ≤ x_k

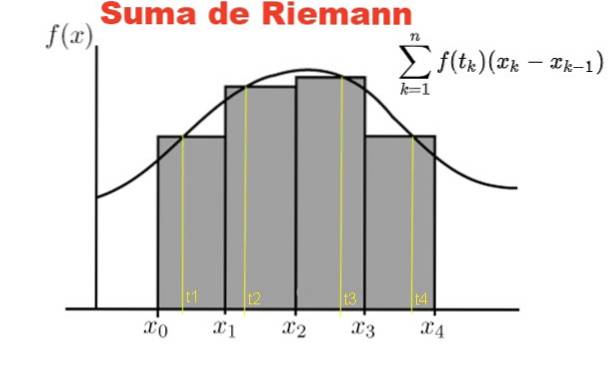
Figur 1 viser grafisk Riemann-summen av funksjonen f på intervallet [x₀, x₄] på en partisjon med fire underintervaller, de grå rektanglene.

Summen representerer det totale arealet til rektanglene, og resultatet av denne summen tilnærmer seg numerisk arealet under kurven f, mellom abscissen x = x₀ y x = x₄.

Selvfølgelig forbedres tilnærmingen til området under kurven sterkt som tallet n skillevegger er større. På denne måten konvergerer summen til området under kurven, når tallet n av partisjoner har en tendens til uendelig.

Artikkelindeks

• 1 Formler og egenskaper
  • 1.1 Arealet under kurven
• 2 Løst øvelser
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referanser

Formler og egenskaper

Riemann-summen av funksjonen f (x) på partisjonen:

P = x₀= a, x₁, x_to,..., x_n= b

Definert på intervallet [a, b], er det gitt av:

S (P, f) = ∑_{k = 1}ⁿ f (t_k) (x_k - x_k-1) 

Hvor T_k er en verdi på intervallet [x_k, x_k-1]. I Riemann-summen brukes vanligvis regelmessige intervaller med bredde Δx = (b - a) / n, der a og b er minimums- og maksimumsverdiene til abscissen, mens n er antall underavdelinger.

I så fall Riemann riktig sum Det er:

Sd (f, n) = [f (a + Δx) + f (a + 2Δx) +… + f (a + (n-1) Δx) + f (b)] * Δx

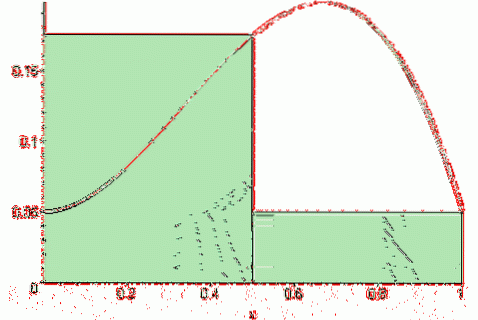
Mens Riemann la igjen summen uttrykkes som:

Hvis (f, n) = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx

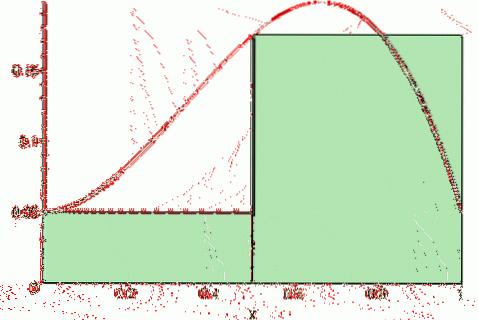
Endelig sentrale Riemann sum Det er:

Sc (f, n) = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx

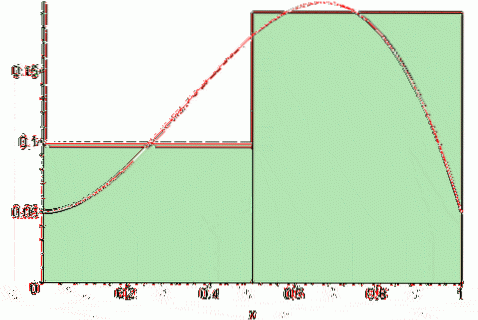
Avhengig av hvor punktet t ligger_k på intervallet [x_k, x_k-1] Riemann-summen kan overvurdere eller undervurdere den nøyaktige verdien av området under kurven til funksjonen y = f (x). Med andre ord kan rektanglene stikke ut fra kurven eller være litt under den..

Området under kurven

Hovedegenskapen til Riemann-summen og som dens betydning kommer fra, er at hvis antallet underavdelinger har en tendens til uendelig, konvergerer resultatet av summen til den bestemte integralen av funksjonen:

Løst øvelser

- Øvelse 1

Beregn verdien av den bestemte integralen mellom a = -2 til b = +2 av funksjonen:

f (x) = x^to

Benytt deg av en Riemann-sum. For å gjøre dette, finn først summen for n vanlige partisjoner av intervallet [a, b] og ta deretter den matematiske grensen for det tilfellet at antall partisjoner har en tendens til uendelig. 

Løsning

Dette er trinnene du må følge:

-Først definerer du intervallet til partisjonene som: 

Δx = (b - a) / n. 

-Da ser Riemann-summen fra høyre som tilsvarer funksjonen f (x) slik ut:

[-2 + (4i / n)]^to = 4 - (16 i / n) + (4 / n)^to Jeg^to

-Og så er det nøye erstattet i summeringen:

-Det neste trinnet er å skille summasjonene og ta de konstante mengdene som en felles faktor for hver sum. Det er nødvendig å ta i betraktning at indeksen er i, derfor tallene og vilkårene med n betraktes som konstant:

-Hver summering blir evaluert, siden det er passende uttrykk for hver av dem. For eksempel gir den første av summene n:

S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6n^to

-Til slutt har vi at integralen vi ønsker å beregne er:

= 16 - (64/2) + (64/3) = 16/3 = 5.333

Leseren kan verifisere at dette er det nøyaktige resultatet, som kan oppnås ved å løse den ubestemte integralen og evaluere grensene for integrering etter Barrow's regel.

- Øvelse 2

Omtrent bestemme området under funksjonen: 

f (x) = (1 / √ (2π)) e^(-xto/to)

Skriv inn x = -1 og x = + 1, ved hjelp av en sentral Riemann-sum med 10 partisjoner. Sammenlign med det eksakte resultatet og estimer prosentandelen forskjellen.

Løsning

Trinnet eller trinnet mellom to påfølgende diskrete verdier er:

Δx = (1 - (-1) / 10 = 0,2

Så partisjonen P som rektanglene er definert på ser slik ut:

P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Men siden det som er ønsket er den sentrale summen, vil funksjonen f (x) bli evaluert ved midtpunktene til delintervallene, det vil si i settet:

T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0.9.

Den (sentrale) Riemann-summen ser slik ut:

S = f (-0,9) * 0,2 + f (-0,7) * 0,2 + f (-0,5) * 0,2 +… + f (0,7) * 0,2 + f (0,9) * 0,2

Siden funksjonen f er symmetrisk, er det mulig å redusere summen til bare 5 termer, og resultatet multipliseres med to:

S = 2 * 0,2 * f (0,1) + f (0,3) + f (0,5) + f (0,7) + f (0,9)

S = 2 * 0,2 * 0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funksjonen gitt i dette eksemplet er ingen ringere enn den velkjente Gauss-klokken (normalisert, med gjennomsnitt lik null og standardavvik en). Arealet under kurven i intervallet [-1,1] for denne funksjonen er kjent for å være 0,6827.

Dette betyr at den omtrentlige løsningen med bare 10 termer samsvarer med den eksakte løsningen med tre desimaler. Prosentandelen feil mellom den omtrentlige og den nøyaktige integralen er 0,07%.

Referanser

1. Casteleiro, J. M. og Gómez-Álvarez, R. P. (2002). Integral calculus (Illustrert utg.). Madrid: ESIC-redaksjon.
2. Unican. Historien om begrepet integral. Gjenopprettet fra: repositorio.unican.es
3. UIS. Summerer Riemann. Gjenopprettet fra: matematicas.uis.edu.co
4. Wikipedia. Riemann sum. Gjenopprettet fra: es.wikipedia.com
5. Wikipedia. Riemann-integrering. Gjenopprettet fra: es.wikipedia.com