
Teori om karakteristiske sett, elementer, eksempler, øvelser
De mengde teori Det er en gren av logikk-matematikk som er ansvarlig for studiet av forholdet mellom enheter som kalles sett. Settene er preget av å være samlinger av gjenstander av samme natur. Disse objektene er elementene i settet og kan være: tall, bokstaver, geometriske figurer, ord som representerer objekter, objektene selv og andre.
Det var Georg Cantor mot slutten av 1800-tallet som foreslo mengde teori. Mens andre bemerkelsesverdige matematikere i det 20. århundre gjorde formaliseringen: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel blant andre..

Venn-diagrammer er den grafiske måten å representere et sett på, og det består av en lukket planfigur der elementene i settet er.
I figur 1 vises for eksempel to sett A og B, som har elementer til felles, elementene som er felles for A og B. Disse danner et nytt sett som kalles skjæringssettet A og B, som er skrevet i formen symbolsk som følger:
A ∩ B
Artikkelindeks
- 1 Funksjoner
- 2 typer sett
- 2.1 Endelig sett
- 2.2 Uendelig sett
- 2.3 Tomt sett
- 2.4 Enhetssett
- 2.5 Binærsett
- 2.6 Universalsett
- 3 grunnleggende elementer
- 3.1 - Forholdet mellom sett
- 3.2 - Egenskaper for inkludering
- 3.3 - Operasjoner mellom sett
- 4 Eksempler
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 4.3 Eksempel 3
- 4.4 Eksempel 4
- 4.5 Eksempel 5
- 5 Øvelser løst
- 5.1 Øvelse 1
- 5.2 Øvelse 2
- 5.3 Øvelse 3
- 5.4 Øvelse 4
- 6 Referanser
Kjennetegn
Settet er et primitivt konsept som det er i geometri begrepet punkt, linje eller plan. Det er ingen bedre måte å uttrykke konseptet på enn å peke på eksempler:
Sett E dannet av fargene på Spanias flagg. Denne måten å uttrykke settet på kalles forståelse. Det samme settet E skrevet med forlengelse er:
E = rød, gul
I dette tilfellet er rød og gul elementer i sett E. Det skal bemerkes at elementene er oppført i bukseseler og ikke gjentas. Når det gjelder det spanske flagget, er det tre fargede striper (rød, gul, rød), hvorav to gjentas, men elementene blir ikke gjentatt når settet uttrykkes..
Anta at settet V dannet av de tre første vokalbokstavene:
V = a, e, i
Kraftsettet til V, betegnet med P (V) er settet med alle sett som kan dannes med elementene i V:
P (V) = a, e, i, a, e, a, i, e, i, a, e, i
Typer sett
Endelig sett
Det er et sett der elementene er tellbare. Eksempler på endelige sett er bokstavene i det spanske alfabetet, vokalene på spansk, planetene i solsystemet, blant andre. Antall elementer i et endelig sett kalles kardinaliteten.
Uendelig sett
Et uendelig sett er forstått som alt at antallet av elementene er utallige, siden uansett hvor stort antall elementer det kan være, er det alltid mulig å finne flere elementer.
Et eksempel på et uendelig sett er settet med naturlige tall N, som i omfattende form uttrykkes som følger:
N = 1, 2, 3, 4, 5,…. Er helt klart et uendelig sett, siden uansett hvor stort et naturlig tall kan være, kan det nest største alltid bli funnet, i en endeløs prosess. Det er tydelig at kardinaliteten til et uendelig sett er ∞.
Tomt sett
Det er settet som ikke inneholder noe element. Det tomme settet V er betegnet med Ø eller med et par nøkler uten elementer inni:
V = = Ø.
Det tomme settet er unikt, derfor må det være feil å si "et tomt sett", det riktige skjemaet er å si "det tomme settet".
Blant egenskapene til det tomme settet har vi at det er en delmengde av ethvert sett:
Ø ⊂ A
Videre, hvis et sett er en delmengde av det tomme settet, vil nødvendigvis nevnte sett være vakuumet:
A ⊂ Ø ⇔ A = Ø
Enhetlig sett
Et enhetssett er ethvert sett som inneholder et enkelt element. For eksempel er settet med naturlige satellitter på jorden et enhetlig sett, hvis eneste element er månen. Settet B med heltall mindre enn 2 og større enn null har bare element 1, derfor er det et enhetlig sett.
Binær sett
Et sett er binært hvis det bare har to elementer. For eksempel settet X, slik at x er en reell tallløsning på x ^ 2 = 2. Dette settet ved forlengelse er skrevet slik:
X = -√2, + √2
Universal sett
Det universelle settet er et sett som inneholder andre sett av samme type eller natur. For eksempel er det universelle settet med naturlige tall settet med reelle tall. Men de reelle tallene er et universelt sett også av heltall og rasjonelle tall.
Kjerneartikler
- Forholdet mellom sett
I forsamlinger kan forskjellige typer forhold etableres mellom dem og deres elementer. Hvis to sett A og B har nøyaktig de samme elementene mellom seg, etableres et likhetsforhold, betegnet som følger:
TIL = B
Hvis alle elementene i et sett A tilhører et sett B, men ikke alle elementene i B tilhører A, er det mellom disse settene en inkluderingsrelasjon som er betegnet slik:
A ⊂ B, men B ⊄ A
Ovennevnte uttrykk lyder: A er en delmengde av B, men B er ikke en delmengde av A.
For å indikere at noen eller noen elementer tilhører et sett, brukes medlemskapssymbolet ∈, for eksempel å si at x-element eller elementer tilhører settet A er skrevet symbolsk slik:
x ∈ A
Hvis et element ikke tilhører mengden A, skrives denne relasjonen slik:
og ∉ A
Medlemskapsforholdet oppstår mellom elementene i et sett og settet, med det eneste unntaket for kraftsettet, hvor kraftsettet er samlingen eller settet av alle mulige sett som kan dannes med elementene i settet.
Anta at V = a, e, i, dens kraft er P (V) = a, e, i, a, e, a, i, e, i , a, e, i, i dette tilfellet blir settet V et element i settet P (V) og kan skrives:
V ∈ P (V)
- Inkluderingsegenskaper
Den første egenskapen til inkludering fastslår at hvert sett er inneholdt i seg selv, eller med andre ord, at det er en delmengde av seg selv:
A ⊂ A
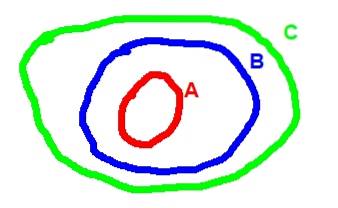
Den andre egenskapen ved inkludering er transitivitet: hvis A er en delmengde av B og B i sin tur er en delmengde av C, så er A en delmengde av C. I symbolsk form skrives transitivitetsrelasjonen slik:
(A ⊂ B) ^ (B ⊂ C) => A ⊂ C
Nedenfor er Venn-diagrammet som tilsvarer transittiviteten til inkludering:
- Operasjoner mellom sett
Kryss
Krysset er en operasjon mellom to sett som gir opphav til et nytt sett som tilhører det samme universelle settet som de to første. Sånn sett er det en lukket operasjon.
Symbolsk er skjæringsoperasjonen formulert slik:
A⋂B = x / x∈A ^ x∈B
Et eksempel er følgende: mengden A av bokstavene til i ordet "elementer" og mengde B for bokstavene for ordet "gjentatt", skjæringspunktet mellom A og B er skrevet slik:
A⋂B = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s. Det universelle settet U av A, av B og også av A⋂B er settet med bokstavene i det spanske alfabetet.
Union
Foreningen av to sett er settet som dannes av elementene som er felles for de to settene og de ikke-vanlige elementene i de to settene. Forbundsoperasjonen mellom sett uttrykkes symbolsk slik:
A∪B = x / x∈A v x∈B
Forskjell
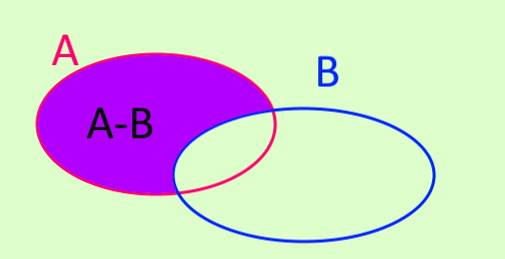
Differensoperasjonen av sett A minus sett B er betegnet med A-B. A-B er et nytt sett dannet av alle elementene som er i A og som ikke tilhører B. Symbolsk er det skrevet slik:
A - B = x / x ∈ A ^ x ∉ B
Symmetrisk forskjell
Den symmetriske forskjellen er en operasjon mellom to sett der det resulterende settet består av elementene som ikke er felles for de to settene. Den symmetriske forskjellen er symbolsk representert slik:
A⊕B = x / x∈ (A-B) ^ x∈ (B-A)
Eksempler
Eksempel 1
Venn-diagrammet er en grafisk måte å representere sett på. For eksempel er settet C for bokstavene i ordsettet representert slik:

Eksempel 2
Det er vist nedenfor av Venn-diagrammer at vokalsett i ordet "sett" er en delmengde av bokstavsettet i ordet "sett".

Eksempel 3
Sett Ñ av bokstavene i det spanske alfabetet er et endelig sett, dette settet som forlengelse er skrevet slik:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z og dens kardinalitet er 27.
Eksempel 4
Sett V av vokalene på spansk er en delmengde av settet Ñ:
V ⊂ Ñ derfor er det et endelig sett.
Det endelige settet V i omfattende form er det skrevet slik: V = a, e, i, o, u og dens kardinalitet er 5.
Eksempel 5
Gitt settene A = 2, 4, 6, 8 og B = 1, 2, 4, 7, 9 bestem A-B og B-A.
A - B er elementene i A som ikke er i B:
A - B = 6, 8
B - A er elementene i B som ikke er i A:
B - A = 1, 7, 9
Løst øvelser
Øvelse 1
Skriv i symbolsk form og også i utvidelse settet P med jevne naturlige tall mindre enn 10.
Løsning: P = x∈ N / x < 10 ^ x mod 2 = 0
P = 2, 4, 6, 8
Øvelse 2
Anta mengden A som dannes av de naturlige tallene som er faktorene 210, og mengden B som dannes av de primære naturlige tallene mindre enn 9. Bestem ved å utvide begge mengdene og fastslå hvilket forhold det er mellom de to settene.
Løsning: For å bestemme elementene i sett A, må vi begynne med å finne faktorene til det naturlige tallet 210:
210 = 2 * 3 * 5 * 7
Så settes sett A:
A = 2, 3, 5, 7
Vi betrakter nå settet B, som er primtallene mindre enn 9. 1 er ikke primtall fordi det ikke oppfyller definisjonen av primtall: "et tall er prime hvis og bare hvis det har nøyaktig to delere, 1 og selve tallet" . 2 er jevn og samtidig er den primær fordi den oppfyller definisjonen av prim, de andre primtalene mindre enn 9 er 3, 5 og 7. Så sett B er:
B = 2, 3, 5, 7
Derfor er de to settene like: A = B.
Øvelse 3
Bestem settet der elementene x er forskjellige fra x.
Løsning: C = x / x ≠ x
Siden hvert element, tall eller objekt er lik seg selv, kan settet C ikke være annet enn det tomme settet:
C = Ø
Øvelse 4
La settet til N av naturlige tall og Z være settet med heltall. Bestem N ⋂ Z og N ∪ Z.
Løsning:
N ⋂ Z = x ∈ Z / x ≤ 0 = (-∞, 0]
N ∪ Z = Z fordi N ⊂ Z.
Referanser
- Garo, M. (2014). Matematikk: kvadratiske ligninger: Hvordan løse en kvadratisk ligning. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matematikk for ledelse og økonomi. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matematikk 1 SEP. Terskel.
- Preciado, C. T. (2005). Matematikkurs 3.. Redaksjonell Progreso.
- Matematikk 10 (2018). "Eksempler på endelige sett". Gjenopprettet fra: matematicas10.net
- Wikipedia. Settteori. Gjenopprettet fra: es.wikipedia.com


Ingen har kommentert denne artikkelen ennå.