
Bayes teorem forklaring, applikasjoner, øvelser
De Bayes teorem er en prosedyre som lar oss uttrykke den betingede sannsynligheten for en tilfeldig hendelse A gitt B, når det gjelder sannsynlighetsfordelingen av hendelse B gitt A og sannsynlighetsfordelingen på bare A.
Denne setningen er veldig nyttig, siden takket være den kan vi relatere sannsynligheten for at en hendelse A inntrer, vel vitende om at B skjedde, med sannsynligheten for at det motsatte oppstår, det vil si at B forekommer gitt.
Bayes teorem var et sølvforslag fra pastor Thomas Bayes, en engelsk teolog fra 1700-tallet som også var matematiker. Han var forfatter av flere verk i teologien, men for tiden er han kjent for et par matematiske avhandlinger, deriblant den allerede nevnte Bayes-teorem skiller seg ut som hovedresultatet.
Bayes behandlet denne teoremet i et verk med tittelen "An Essay towards solving a Problem in the Doctrine of Chances", publisert i 1763, og som det er utviklet et stort antall studier med applikasjoner innen ulike kunnskapsområder..
Artikkelindeks
- 1 Forklaring
- 2 Anvendelser av Bayes 'teorem
- 2.1 Løste øvelser
- 3 Referanser
Forklaring
For det første, for å få en bedre forståelse av denne teoremet, er noen grunnleggende forestillinger om sannsynlighetsteori nødvendig, spesielt multiplikasjonssatsen for betinget sannsynlighet, som sier at
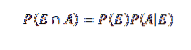
For E og A vilkårlige hendelser i et prøveområde S.
Og definisjonen av partisjoner, som forteller oss at hvis vi har A1 ,TILto,… , TILn hendelser i et prøveområde S, vil disse danne en partisjon av S, hvis AJeg er gjensidig utelukkende og deres forening er S.
Gitt dette, la B være en annen begivenhet. Så vi kan se B som
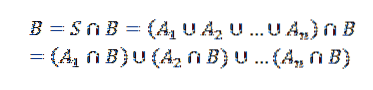
Hvor AJeg krysset med B er gjensidig utelukkende hendelser.
Og i konsekvens,
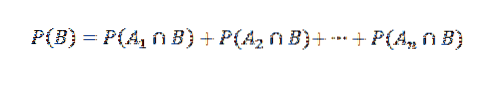
Bruk deretter multiplikasjonssatsen
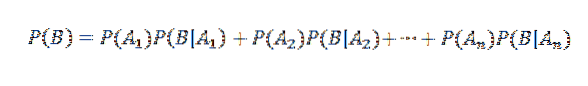
På den annen side er den betingede sannsynligheten for Ai gitt B definert av
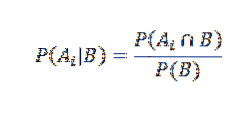
Ved å erstatte riktig har vi det for alle i
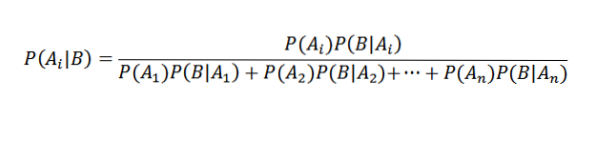
Anvendelser av Bayes 'teorem
Takket være dette resultatet har forskergrupper og ulike selskaper klart å forbedre systemer som er basert på kunnskap..
I studien av sykdommer kan Bayes 'teorem for eksempel bidra til å skille sannsynligheten for at en sykdom blir funnet i en gruppe mennesker med en gitt karakteristikk, og ta som data de globale hastighetene på sykdommen og overvekten av nevnte egenskaper i begge sunne og syke mennesker.
På den annen side, i verden av høyteknologier, har den påvirket store selskaper som takket være dette resultatet har utviklet "kunnskapsbasert" programvare.
Som et daglig eksempel har vi Microsoft Office-assistenten. Bayes teorem hjelper programvaren med å evaluere problemene som brukeren presenterer og bestemme hvilke råd de skal gi og dermed kunne tilby en bedre service i henhold til brukerens vaner.
Det skal bemerkes at denne formelen ble ignorert inntil nylig, dette er hovedsakelig fordi da dette resultatet ble utviklet for 200 år siden, var det lite praktisk bruk for dem. Men i vår tid, takket være store teknologiske fremskritt, har forskere funnet måter å praktisere dette resultatet på.
Løste øvelser
Øvelse 1
Et mobiltelefonselskap har to maskiner A og B. 54% av produserte mobiltelefoner er produsert av maskin A og resten av maskin B. Ikke alle produserte mobiltelefoner er i god stand.
Andelen defekte mobiltelefoner laget av A er 0,2 og av B er 0,5. Hva er sannsynligheten for at en mobiltelefon fra den fabrikken er defekt? Hva er sannsynligheten for at, vel vitende om at en mobiltelefon er defekt, kommer den fra maskin A?
Løsning
Her har du et eksperiment som er utført i to deler; i første del skjer hendelsene:
A: celle laget av maskin A.
B: celle laget av maskin B.
Siden maskin A produserer 54% av mobiltelefoner og resten produseres av maskin B, følger det at maskin B produserer 46% av mobiltelefoner. Sannsynlighetene for disse hendelsene er gitt, nemlig:
P (A) = 0,54.
P (B) = 0,46.
Hendelsene i andre del av eksperimentet er:
D: defekt mobiltelefon.
E: ikke-defekt mobiltelefon.
Som nevnt i uttalelsen, er sannsynligheten for disse hendelsene avhengig av resultatet oppnådd i første del:
P (D | A) = 0,2.
P (D | B) = 0,5.
Ved å bruke disse verdiene kan sannsynligheten for komplementene til disse hendelsene også bestemmes, det vil si:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
Y
p (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Nå kan begivenhet D skrives som følger:
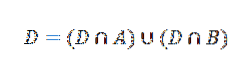
Bruke multiplikasjonssatsen for betingede sannsynlighetsresultater:
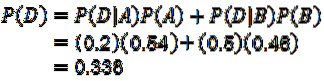
Som det første spørsmålet blir besvart med.
Nå trenger vi bare å beregne P (A | D), som Bayes-teoremet gjelder for:
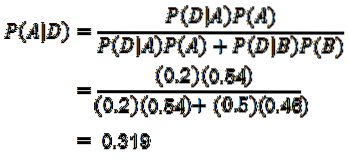
Takket være Bayes 'teorem kan det fastslås at sannsynligheten for at en mobiltelefon er laget av maskin A, vel vitende om at mobiltelefonen er defekt, er 0,319.
Øvelse 2
Tre bokser inneholder svarte og hvite kuler. Sammensetningen av hver av dem er som følger: U1 = 3B, 1N, U2 = 2B, 2N, U3 = 1B, 3N.
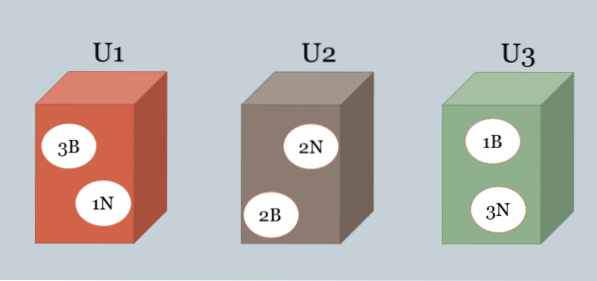
En av boksene er valgt tilfeldig og en ball trekkes tilfeldig som viser seg å være hvit. Hva er boksen mest sannsynlig å ha blitt valgt?
Løsning
Ved å bruke U1, U2 og U3, vil vi også representere den valgte boksen.
Disse hendelsene utgjør en partisjon av S og det er bekreftet at P (U1) = P (U2) = P (U3) = 1/3 siden valget av ruten er tilfeldig.
Hvis B = den trukkede ballen er hvit, vil vi ha P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Det vi ønsker å oppnå er sannsynligheten for at ballen er tatt ut av boksen Ui, vel vitende om at ballen var hvit, det vil si P (Ui | B), og se hvilken av de tre verdiene som var høyest å vite hvor boksen mest sannsynlig har vært utvinning av den hvite kulen.
Bruk av Bayes teorem på den første av boksene:
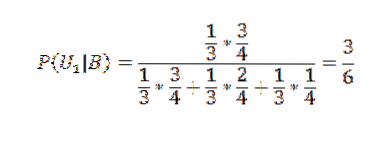
Og for de to andre:
P (U2 | B) = 2/6 og P (U3 | B) = 1/6.
Så er den første av boksene den med størst sannsynlighet for å være valgt for utvinning av den hvite kulen..
Referanser
- Kai Lai Chung. Elementær sannsynlighetsteori med stokastiske prosesser. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskret matematikk og dens applikasjoner. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannsynlighet og statistiske applikasjoner. S.A. MEKSIKANSK ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Løste problemer med diskret matematikk. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori og sannsynlighetsproblemer. McGRAW-HILL.



Ingen har kommentert denne artikkelen ennå.