
Euclids teorem Bevis, anvendelse og øvelser
De Euklids teorem demonstrerer egenskapene til en høyre trekant ved å tegne en linje som deler den i to nye høyre trekanter som ligner på hverandre og som igjen ligner på den opprinnelige trekanten; så er det et forhold av proporsjonalitet.
Euclid var en av de største matematikerne og geometrikerne i eldgamle tider som utførte flere bevis på viktige teoremer. En av de viktigste er den som bærer navnet hans, som har hatt en bred anvendelse.

Dette har vært tilfelle fordi det gjennom denne teoremet på en enkel måte forklarer de geometriske forholdene som eksisterer i den rette trekanten, hvor beina til dette er relatert til deres fremskrivninger i hypotenusen..
Artikkelindeks
- 1 Formler og bevis
- 1.1 Høyde setning
- 1.2 Legsteorem
- 2 Forholdet mellom Euklids teoremer
- 3 Løst øvelser
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Referanser
Formler og demonstrasjon
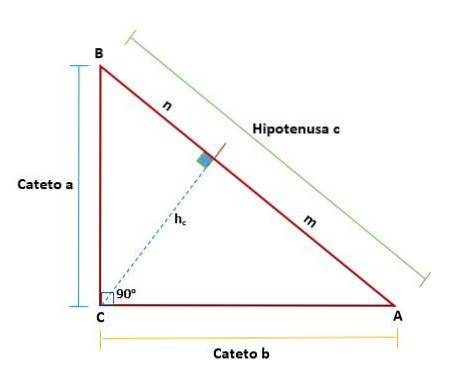
Euklids teorem foreslår at i hver rette trekant, når en linje tegnes - som representerer høyden som tilsvarer toppunktet for den rette vinkelen i forhold til hypotenusen - dannes to høyre trekanter fra originalen.
Disse trekantene vil være lik hverandre og vil også være lik den opprinnelige trekanten, noe som betyr at deres like sider er proporsjonale med hverandre:
Vinklene til de tre trekantene er kongruente; det vil si når de roteres 180 grader rundt toppunktet, faller den ene vinkelen sammen med den andre. Dette innebærer at de alle vil være de samme.
På denne måten kan likheten som eksisterer mellom de tre trekantene også verifiseres ved likeverdene i deres vinkler. Fra likheten mellom trekanter, etablerer Euclid andelene av disse fra to teoremer:
- Høyde setning.
- Legsetning.
Denne teoremet har en bred anvendelse. I eldgamle tider ble den brukt til å beregne høyder eller avstander, noe som representerte et stort fremskritt for trigonometri.
Den brukes for tiden på forskjellige områder som er basert på matematikk, som ingeniørfag, fysikk, kjemi og astronomi, blant mange andre områder..
Høyde setning
I denne teoremet fastslås det at i en hvilken som helst rett trekant er høyden tegnet fra rett vinkel i forhold til hypotenusen det geometriske proporsjonale gjennomsnittet (kvadratet av høyden) mellom benprojeksjonene som den bestemmer på hypotenus.
Det vil si at høydens kvadrat vil være lik multiplikasjonen av de projiserte beina som danner hypotenusen:
hcto = m * n
Demonstrasjon
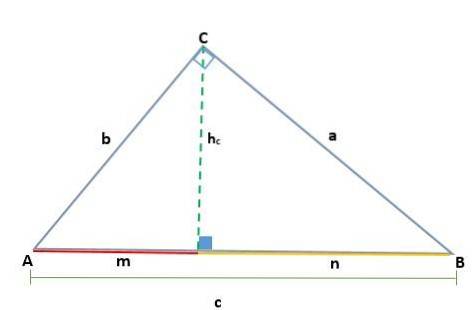
Gitt en trekant ABC, som er rett ved toppunkt C, genererer tegning av høyden to like høyre trekanter, ADC og BCD; derfor er deres tilsvarende sider proporsjonale:
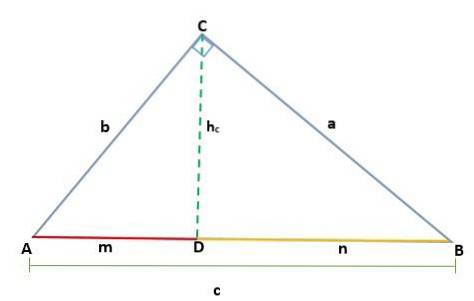
På en slik måte at høyden hc som tilsvarer segmentet CD, tilsvarer hypotenusen AB = c, derfor har vi:
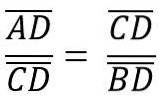
I sin tur tilsvarer dette:
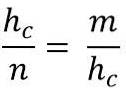
Løsning for hypotenusen (hc), for å multiplisere de to medlemmene av likheten, må vi:
hc * hc = m * n
hcto = m * n
Dermed er verdien av hypotenusen gitt av:
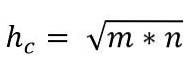
Legsetning
I denne teoremet er det fastslått at målet i hvert ben i hver rette trekant vil være det geometriske proporsjonale gjennomsnittet (kvadratet på hvert ben) mellom målet på hypotenusen (komplett) og projeksjonen til hver enkelt på den:
bto = c * m
tilto = c* n
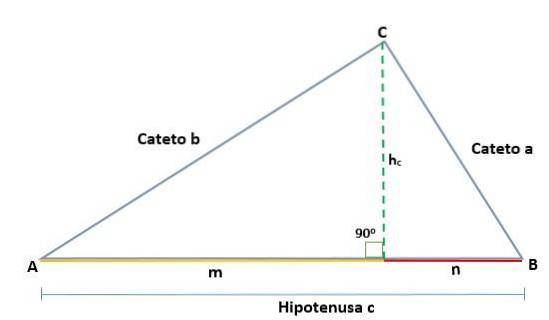
Demonstrasjon
Gitt en trekant ABC, som er rett ved toppunktet C, på en slik måte at dens hypotenus er c, når man tegner høyden (h) bestemmes fremspringene til bena a og b, som er henholdsvis segmentene m og n, og som ligger på hypotenusen.
Dermed har vi at høyden tegnet på høyre trekant ABC genererer to like høyre trekanter, ADC og BCD, slik at de tilsvarende sidene er proporsjonale, slik:
DB = n, som er projeksjonen av ben CB på hypotenusen.
AD = m, som er projeksjonen av benet AC på hypotenusen.
Deretter bestemmes hypotenusen c av summen av beina på projeksjonene:
c = m + n
På grunn av likheten mellom trekantene ADC og BCD har vi:
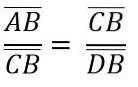
Ovennevnte er det samme som:
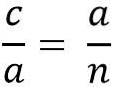
Å løse etappe “a” for å multiplisere de to medlemmene av likheten, har vi:
til * a = c * n
tilto = c * n
Verdien av etappe "a" er således gitt av:
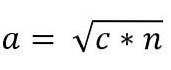
På samme måte, på grunn av likheten mellom trekantene ACB og ADC, har vi:
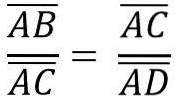
Ovennevnte er lik:
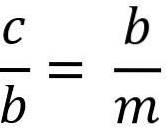
Å løse etappe "b" for å multiplisere de to medlemmene av likheten, har vi:
b * b = c * m
bto = c * m
Verdien av etappe "b" er således gitt av:
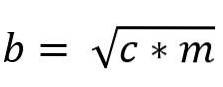
Forholdet mellom Euklids teoremer
Setningene med referanse til høyden og bena er relatert til hverandre fordi målene for begge er laget med hensyn til hypotenusen til høyre trekant.
Gjennom forholdet til Euklids teoremer kan verdien av høyden også bli funnet; dette er mulig ved å løse verdiene til m og n fra leggsetningen, og de erstattes i høydesetningen. På denne måten er det tilfreds at høyden er lik multiplikasjonen av bena, delt på hypotenusen:
bto = c * m
m = bto ÷ c
tilto = c * n
n = ato ÷ c
I høydesetningen erstatter vi m og n:
hcto = m * n
hcto = (bto ÷ c) * (tilto ÷ c)
hc = (bto * tilto) ÷ c
Løst øvelser
Eksempel 1
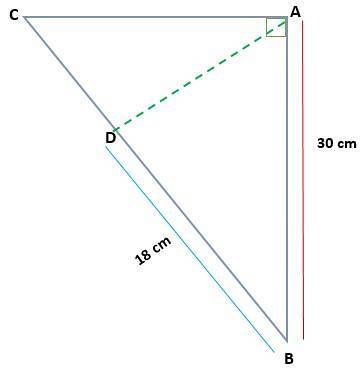
Gitt trekanten ABC, rett ved A, bestem målingen på AC og AD, hvis AB = 30 cm og BD = 18 cm
Løsning
I dette tilfellet har vi målingene på et av de projiserte beina (BD) og et av beina til den opprinnelige trekanten (AB). På denne måten kan benteoremet brukes for å finne verdien av beinet BC.
ABto = BD * F.Kr.
(30)to = 18 * F.Kr.
900 = 18 * F.Kr.
BC = 900 ÷ 18
BC = 50 cm
Verdien av bein-CD-en kan bli funnet å vite at BC = 50:
CD = BC - BD
CD = 50 - 18 = 32 cm
Nå er det mulig å bestemme verdien av beinet AC, ved å bruke bensetningen på nytt:
ACto = CD * BD
ACto = 32 * femti
ACto = 160
AC = √1600 = 40 cm
For å bestemme verdien av høyden (AD) brukes høydesetningen, siden verdiene til de projiserte bena CD og BD er kjent:
ADto = 32 * 18
ADto = 576
AD = √576
AD = 24 cm
Eksempel 2
Bestem verdien av høyden (h) til en trekant MNL, rett i N, og kjenn til målene til segmentene:
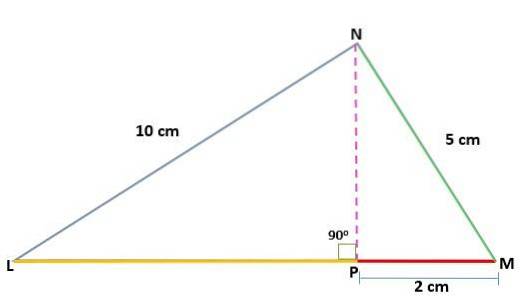
NL = 10 cm
MN = 5 cm
PM = 2 cm
Løsning
Vi har mål på et av bena projisert på hypotenusen (PM), så vel som målene på bena til den opprinnelige trekanten. På denne måten kan legsetningen brukes for å finne verdien av det andre projiserte beinet (LN):
NLto = PM * LM
(10)to = 5 * LM
100 = 5 * LM
PL = 100 ÷ 5 = 20
Ettersom verdien av beina og hypotenusen allerede er kjent, kan verdien av høyden bestemmes gjennom forholdet mellom setningene i høyden og bena:
NL = 10
MN = 5
LM = 20
h = (bto * tilto) ÷ c.
h = (10to * 5to) ÷ (tjue)
h = (100 * 25) ÷ (tjue)
h = 2500 ÷ tjue
h = 125 cm.
Referanser
- Braun, E. (2011). Kaos, fraktaler og rare ting. Fond for økonomisk kultur.
- Cabrera, V. M. (1974). Moderne matematikk, bind 3.
- Daniel Hernandez, D. P. (2014). 3. års matematikk. Caracas: Santillana.
- Encyclopaedia Britannica, i. (nitten nitti fem). Hispanic Encyclopedia: Macropedia. Encyclopedia Britannica Publishers.
- Euclid, R. P. (1886). Euclids elementer av geometri.
- Guardeño, A. J. (2000). Arven fra matematikk: fra Euclid til Newton, geniene gjennom bøkene sine. Sevilla universitet.



Ingen har kommentert denne artikkelen ennå.