
Tredje lov om termodynamikk formler, ligninger, eksempler
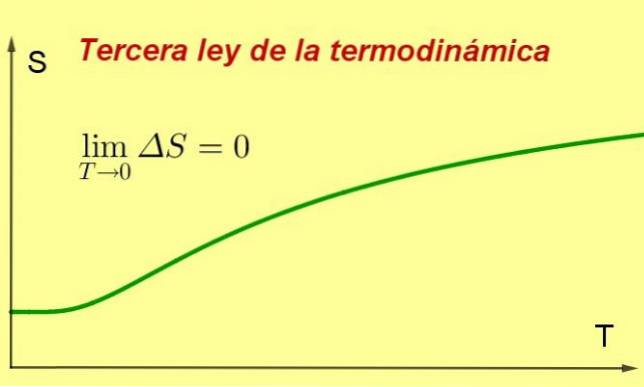
De Tredje lov om termodynamikk sier at entropien til et lukket termodynamisk system i likevekt har en tendens til å være minimal og konstant, ettersom temperaturen nærmer seg 0 kelvin.
Denne entropiværdien vil være uavhengig av systemvariablene (trykk eller påført magnetfelt, blant andre). Det som skjer er at når temperaturen er nærmere 0 K, stopper prosessene i systemet, og da entropi er et mål på intern agitasjon, faller det nødvendigvis.
Artikkelindeks
- 1 Tidligere konsepter
- 1.1 Termodynamisk system
- 1.2 Isolerte, lukkede eller åpne systemer
- 1.3 Makrostater og mikrostater
- 2 Formler og ligninger
- 2.1 Beregning av absolutt entropi av et stoff
- 3 applikasjoner
- 3.1 Entropi av et system ved lav temperatur
- 3.2 Rest entropi
- 4 Eksempler
- 4.1 Eksempel 1: absolutt null og Heisenbergs ubestemmelighet
- 4.2 Eksempel 2: Overflødighet og det rare merket med helium-4
- 5 Øvelser løst
- 5.1 - Øvelse 1
- 5.2 - Øvelse 2
- 6 Referanser
Tidligere konsepter
For å forstå omfanget av den tredje loven om termodynamikk, relevant ved svært lave temperaturer, er det nødvendig å gjennomgå følgende konsepter:
Termodynamisk system
Henviser generelt til en gass, en væske eller et fast stoff. Det som ikke er en del av systemet kalles miljø. Det vanligste termodynamiske systemet er den ideelle gassen, som består av N-partikler (atomer) som bare samhandler gjennom elastiske kollisjoner.
Isolerte, lukkede eller åpne systemer
Isolerte systemer tillates ikke utveksling med miljøet. Lukkede systemer utveksler ikke materie med miljøet, men de utveksler varme. Til slutt kan åpne systemer utveksle både materie og varme med miljøet..
Makrostatene og mikrostatene
Makrotilstanden til et system er settet med verdier som dets variabler har: trykk, temperatur, volum, antall mol, entropi og intern energi. På den annen side blir mikrostaten - i tilfelle en ideell gass - gitt av posisjonen og momentet til hver av N-partiklene som utgjør den, på et gitt øyeblikk.
Mange mikrostater kan resultere i samme makrostat. I en gass ved romtemperatur er antallet mulige mikrostater enormt, fordi antall partikler som utgjør det, de forskjellige posisjonene og de forskjellige energiene de kan innta er veldig stort..
Formler og ligninger
Entropi, som vi sa, er en termodynamisk makroskopisk variabel som måler graden av molekylær lidelse i systemet. Graden av forstyrrelse i et system er større ettersom antallet mulige mikrostater er større.
Dette konseptet er nødvendig for å formulere den tredje loven om termodynamikk i matematisk form. La S være entropien til systemet, så:

Entropi er en makroskopisk tilstandsvariabel som er direkte relatert til antall mulige mikrostater i et system, gjennom følgende formel:
S = k ln (W)
I ovenstående ligning: S representerer entropi, W antall mulige mikrostater i systemet og k er Boltzmanns konstant (k = 1,38 x 10-2. 3 J / K). Det vil si at entropien til et system er k ganger den naturlige logaritmen til antall mulige mikrostater.
Beregning av den absolutte entropien til et stoff
Det er mulig å definere den absolutte entropien til et rent stoff med utgangspunkt i definisjonen av entropi-variasjonen:

δQ = n. cs .dT
Her er cp molær spesifikk varme og n antall mol. Avhengigheten av molar spesifikk varme med temperatur er data som er innhentet eksperimentelt og kjent for mange rene stoffer..
I henhold til den tredje loven om rene stoffer:


applikasjoner
I hverdagen har den tredje loven om termodynamikk få anvendelser, tvert imot den første og andre loven. Det er fordi det er et prinsipp som refererer til hva som skjer i et system når det nærmer seg absolutt 0, et sjeldent temperaturområde.
Det er faktisk umulig å nå absolutt 0 eller −273.15 ° C (se eksempel 1 nedenfor). Den tredje loven gjelder imidlertid når man studerer materialresponsen ved svært lave temperaturer.
Takket være dette har viktige fremskritt kommet fram i fysikken til kondensert materie, for eksempel:
-Overflødighet (se eksempel 2 nedenfor)
-Superledningsevne
-Laser kjøling teknikker
-Bose-Einstein kondensat
-Fermi superfluid gasser.

Ved ekstremt lave temperaturer tillater reduksjonen i entropi fremveksten av interessante kvantefenomener. La oss derfor se hva som skjer med entropien til et system ved veldig lav temperatur.
Entropi av et system ved lav temperatur
Når du har et perfekt krystallinsk stoff, er dets minimum entropi nøyaktig null, siden det er et høyt ordnet system. Ved temperaturer nær absolutt 0 er materie i kondensert tilstand (flytende eller fast) og vibrasjoner i krystallen er minimale.
Noen forfattere anser en alternativ uttalelse av den tredje loven om termodynamikk som følger:
"Hvis materie kondenserer for å danne en perfekt krystall, når temperaturen har en tendens til absolutt null, har entropien en tendens til nøyaktig null".
La oss avklare noen aspekter av forrige uttalelse:
- En perfekt krystall er en der hvert molekyl er identisk, og hvor molekylstrukturen gjentar seg identisk i sin helhet..
- Når temperaturen nærmer seg absolutt null, reduseres atomvibrasjonen nesten helt.
Da danner krystallet en enkelt konfigurasjon eller mulig mikrostat, det vil si W = 1, og derfor er entropien lik null:
S = k ln (1) = 0
Men det er ikke alltid et materiale som er avkjølt nær absolutt null, danner en krystall, enda mindre er denne krystallen perfekt. Dette skjer bare hvis kjøleprosessen er veldig langsom og reversibel..
Ellers vil faktorer som urenheter i glasset gjøre eksistensen av andre mikrostater mulig. Derfor ville W> 1 og entropien være større enn 0.
Rest entropi
Hvis kjøleprosessen er brå, gjennomgår systemet en rekke ikke-likevektstilstander, som fører til at materialet blir forglasset. I dette tilfellet produseres ikke en ordnet krystallinsk struktur, men et amorft fast stoff, hvis struktur ligner på en væske..
I så fall er ikke minimum entropiværdien i nærheten av absolutt null ikke null, siden antallet mikrostater er betydelig større enn 1. Forskjellen mellom denne entropien og nullentropien i den perfekte krystallinske tilstanden er kjent som gjenværende entropi.
Forklaringen er at under en viss terskeltemperatur har systemet ingen andre muligheter enn å okkupere mikrostatene med lavere energi, som, fordi de er kvantifisert, utgjør et fast antall.
De vil sørge for å holde entropien konstant, selv når temperaturen fortsetter å synke mot absolutt null..
Eksempler
Eksempel 1: absolutt null og Heisenbergs ubestemmelighet
Heisenbergs ubestemmelsesprinsipp fastslår at usikkerheten i posisjonen og momentet til en partikkel, for eksempel i atomene til et krystallgitter, ikke er uavhengige av hverandre, men heller følger følgende ulikhet:
Δx ⋅ Δp ≥ h
Hvor h er Plancks konstant. Det vil si at usikkerheten i posisjon multiplisert med usikkerheten i momentum (masse ganger hastighet) er større enn eller lik Plancks konstant, hvis verdi er veldig liten, men ikke null: h = 6,63 x 10-3. 4 J s.
Og hva har usikkerhetsprinsippet å gjøre med termodynamikkens tredje lov? Hvis atomenes posisjon i krystallgitteret er fast og presis (Δx = 0) da kan hastigheten til disse atomene ta en hvilken som helst verdi mellom 0 og uendelig. Dette motsies av det faktum at ved absolutt null opphører all bevegelse av termisk agitasjon..
Gjensidig, hvis vi antar at ved absolutt null temperatur, opphører all uro og momentet til hvert atom i gitteret er nøyaktig null (Δp = 0), vil Heisenberg usikkerhetsprinsippet antyde at ubestemmelsen i posisjonene til hvert atom ville være uendelig, det vil si at de kan være i hvilken som helst posisjon.
Som en konsekvens av forrige uttalelse, ville antallet mikrostater ha en tendens til uendelig, og entropien ville også ta en ubestemt verdi.
Eksempel 2: Overflødighet og det merkelige tilfellet av helium-4
I superfluiditet, som oppstår ved svært lave temperaturer, mister materie den indre friksjonen mellom molekylene, kalt viskositet. I et slikt tilfelle kan væsken sirkulere uten friksjon for alltid, men problemet er ved disse temperaturene er nesten ingenting flytende bortsett fra helium..
Helium og helium 4 (dens mest utbredte isotop) utgjør et unikt tilfelle, siden helium forblir flytende ved atmosfærisk trykk og temperaturer nær absolutt null..
Når helium-4 blir utsatt for en temperatur under 2,2 K ved atmosfæretrykk blir det a superfluid. Denne oppdagelsen skjedde i 1911 i Leyden av den nederlandske fysikeren Heike Kamerlingh Onnes (1853-1926).
Helium-4-atomet er et boson. Bosoner, i motsetning til fermioner, er partikler som alle kan oppta samme kvantetilstand. Derfor oppfyller ikke bosoner Pauli-utelukkelsesprinsippet.
Da opptar alle helium-4-atomer ved temperaturer under 2,2 K samme kvantetilstand, og det er derfor bare en mulig mikrostat, noe som antyder at superfluid helium-4 har S = 0.
Løst øvelser
- Øvelse 1
La oss se på et enkelt tilfelle som består av et system som bare består av tre partikler som har tre energinivåer. For dette enkle systemet:
a) Bestem antall mulige mikrostater for tre temperaturområder:
-høy
-Halv
-Kort
b) Bestem ved hjelp av Boltzmann-ligningen entropien i de forskjellige temperaturområdene.
c) Diskuter resultatene og forklar om de strider mot den tredje loven om termodynamikk..
Løsning til
På molekylær og atomskala kvantifiseres energiene som et system kan adoptere, noe som betyr at de bare kan ta visse diskrete verdier. I tillegg, når temperaturene er så lave, har partiklene som utgjør systemet bare muligheten til å oppta de laveste energinivåene..
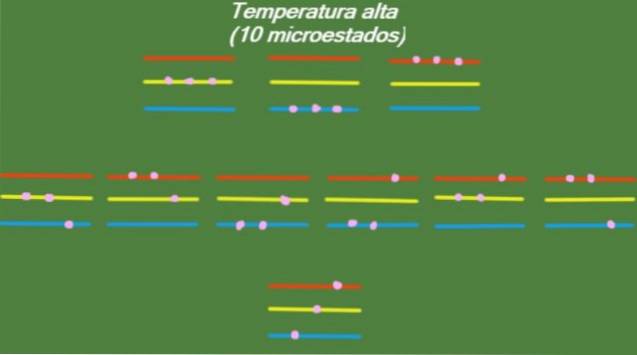
Høy temperatur
Hvis systemet har en relativt høy temperatur T, har partiklene nok energi til å oppta alle tilgjengelige nivåer, noe som gir 10 mulige mikrostater, som vises i følgende figur:
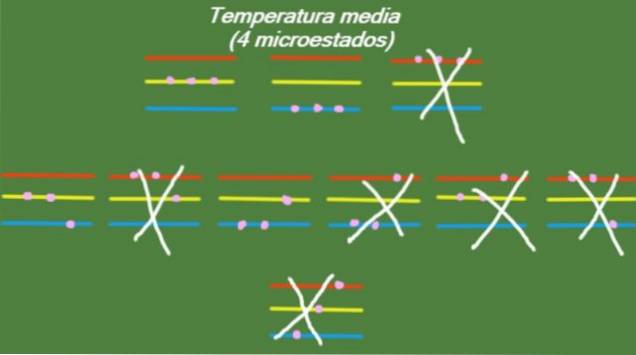
Middels temperatur
I tilfelle at systemet har en mellomtemperatur, har ikke partiklene som utgjør det nok energi til å oppta det høyeste energinivået. De mulige mikrostatene er illustrert i figuren:
Lav temperatur
Hvis temperaturen fortsetter å synke i vårt idealiserte system med tre partikler og tre energinivåer, vil partiklene ha så lite energi at de bare vil kunne oppta det laveste nivået. I dette tilfellet gjenstår bare 1 mulig mikrostatus, som vist i figur 6:
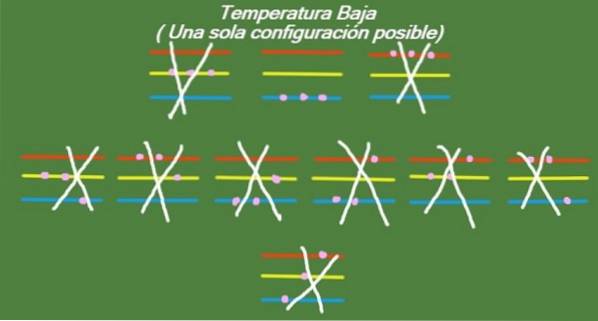
Løsning b
Når antall mikrostater i hvert temperaturområde er kjent, kan vi nå bruke Boltzmann-ligningen gitt ovenfor for å finne entropien i hvert tilfelle.
S = k ln (10) = 2,30 x k = 3,18 x 10-2. 3 J / K (Høy temperatur)
S = k ln (4) = 1,38 x k = 1,92 x 10-2. 3 J / K (Middels temperatur)
Og endelig:
S = k ln (1) = 0 (Lav temperatur)
Løsning c
Først merker vi at entropien synker når temperaturen synker, som forventet. Men for de laveste temperaturverdiene blir en terskelverdi nådd, hvorfra basistilstanden til systemet blir nådd..
Selv når temperaturen er så nær absolutt null som mulig, er det ingen lavere energitilstander tilgjengelig. Så holder entropien minimumsverdien konstant, som i vårt eksempel er S = 0.
Denne øvelsen illustrerer, på mikrostatistikknivå i et system, grunnen til at den tredje loven om termodynamikk holder..
- Øvelse 2
Årsak om følgende utsagn er sant eller usant:
"Entropien til et system ved absolutt null temperatur er nøyaktig null".
Begrunn svaret ditt og beskriv noen eksempler.
Løsning
Svaret er: falsk.
For det første kan den absolutte temperaturen ikke nås fordi den ville bryte Heisenbergs usikkerhetsprinsipp og den tredje loven om termodynamikk..
Det er veldig viktig å merke seg at den tredje loven ikke sier hva som skjer ved absolutt 0, men snarere når temperaturen er uendelig nær absolutt 0. Forskjellen er subtil, men betydelig.
Den tredje loven bekrefter heller ikke at når temperaturen tar en verdi vilkårlig nær absolutt null, har entropien en tendens til null. Dette ville bare skje i tilfellet tidligere analysert: den perfekte krystall, som er en idealisering.
Mange systemer i mikroskopisk skala, det vil si på kvanteskala, har sitt basenivå av energi utartet, som betyr at det eksisterer forskjellige innstillinger på det laveste energinivået.
Dette betyr at entropien i disse systemene aldri ville være nøyaktig null. Entropien ville heller ikke være nøyaktig null i systemer som forglasser når temperaturen har en tendens til absolutt null. I dette tilfellet gjenværende entropi før sett.
Det skyldes at molekylene ble "fast" før de nådde de laveste tilgjengelige energinivåene, noe som betydelig øker antall mulige mikrostater, noe som gjør det umulig for entropien å være nøyaktig null..
Referanser
- Cengel, Y. 2012. Termodynamikk. 7. utgave. McGraw Hill. 347.
- Jet Propulsion Laboratory. Det kuleste stedet i universet. Hentet fra: coldatomlab.jpl.nasa.gov.
- González, A. Entropi og spontanitet. Gjenopprettet fra: geocities.ws
- Quora. Hva er den praktiske bruken av tredje lov om termodynamikk?. Gjenopprettet fra: quora.com
- Generell kjemi. Tredje prinsippet om termodynamikk. Gjenopprettet fra: corinto.pucp.edu.pe
- Tredje lov om termodynamikk. Gjenopprettet fra: youtube.com
- Wikipedia. Rest entropi. Gjenopprettet fra: en.wikipedia.com
- Wikipedia. Tredje lov om termodynamikk. Gjenopprettet fra: en.wikipedia.com

Ingen har kommentert denne artikkelen ennå.