De skrå parabolsk skudd er et spesielt tilfelle av fritt fallbevegelse der prosjektilets utgangshastighet danner en viss vinkel med det horisontale, noe som resulterer i en parabolsk bane.
Fritt fall er et tilfelle av bevegelse med konstant akselerasjon, hvor akselerasjonen er tyngdekraften, som alltid peker vertikalt nedover og har en styrke på 9,8 m / s ^ 2. Det avhenger ikke av prosjektilets masse, slik Galileo Galilei viste i 1604.
Hvis prosjektilets utgangshastighet er loddrett, har fritt fall en rett og vertikal bane, men hvis utgangshastigheten er skrå, er banen for fritt fall en parabolsk kurve, et faktum som også ble demonstrert av Galileo.
Eksempler på parabolsk bevegelse er banen til en baseball, kulen avfyrt fra en kanon og vannstrålen som kommer ut av en slange..
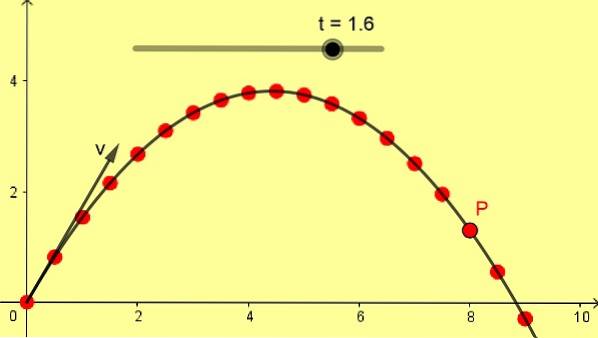
Figur 1 viser et skrått parabelt trekk på 10 m / s med en vinkel på 60º. Skalaen er i meter, og de påfølgende posisjonene til P blir tatt med en differanse på 0,1 s fra det første øyeblikkets 0 sekunder.
Artikkelindeks
Bevegelsen til en partikkel er fullstendig beskrevet hvis dens posisjon, hastighet og akselerasjon er kjent som en funksjon av tiden..
Den parabolske bevegelsen som følge av et skrått skudd er superposisjonen til en horisontal bevegelse med konstant hastighet, pluss en vertikal bevegelse med konstant akselerasjon lik tyngdekraftsakselerasjonen..
Formlene som gjelder for det skrå parabolske utkastet er de som tilsvarer en bevegelse med konstant akselerasjon a = g, Vær oppmerksom på at fet har blitt brukt for å indikere at akselerasjonen er en vektormengde.
I en bevegelse med konstant akselerasjon avhenger posisjonen matematisk av tiden i kvadratisk form.
Hvis vi betegner r(t) stilling til tiden t, reller stillingen i første øyeblikk, veller starthastighet, g akselerasjon og t = 0 som det første øyeblikket formelen som gir posisjonen for hvert øyeblikk t Det er:
r(t) = reller + veller t + ½ g tto
Fet skrift i uttrykket ovenfor indikerer at det er en vektorligning.
Hastigheten som en funksjon av tiden oppnås ved å ta derivatet i forhold til t av posisjonen og resultatet er:
v(t) = veller + g t
Og for å oppnå akselerasjonen som en funksjon av tiden, avledet av hastigheten mht t resulterende:
til(t) = g
Når tid ikke er tilgjengelig, er det et forhold mellom hastighet og posisjon, gitt av:
vto = vellerto - 2 g (og - meg)
Deretter finner vi ligningene som gjelder for et skrått parabolskudd i kartesisk form.
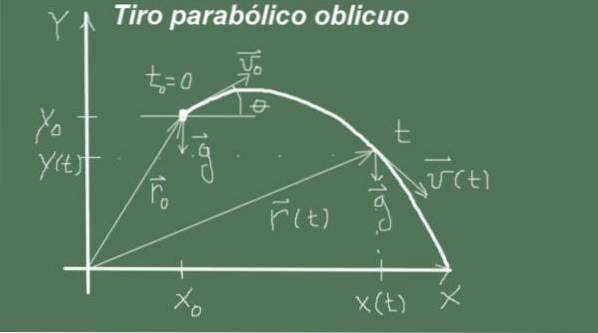
Bevegelsen begynner i øyeblikket t = 0 med startposisjon (xo, meg) og styrke veller og vinkel θ, den første hastighetsvektoren er (veller cosθ, veller senθ). Bevegelsen fortsetter med akselerasjon
g = (0, -g).
Hvis vektorformelen som gir posisjonen som en funksjon av tiden, blir brukt og komponentene er gruppert og utjevnet, vil ligningene som gir koordinatene til posisjonen til enhver tid av tid t oppnås.
x (t) = xeller + vokse t
y (t) = yeller + vHei t -½ g tto
På samme måte har vi ligningene for hastighetskomponentene som en funksjon av tid.
vx(t) = vokse
vY(t) = vHei - g t
Hvor: vokse = veller cosθ; vHei = veller senθ
y = A x ^ 2 + B x + C
A = -g / (2 vokse^ 2)
B = (vHei/ vokse + g xeller/ vokse^ 2)
C = (ogeller - vHei xeller / vokse)
Svar på følgende spørsmål:
a) Hvorfor i parabolske trekkproblemer blir effekten av friksjon med luft vanligvis neglisjert??
b) Har formen på objektet noen betydning i parabolskuddet?
a) For at et prosjektils bevegelse skal være parabolsk, er det viktig at luftens friksjonskraft er mye mindre enn vekten av gjenstanden som kastes.
Hvis en korkekule eller noe lett materiale kastes, er friksjonskraften sammenlignbar med vekten, og dens bane kan ikke nærme seg en parabel.
Tvert imot, hvis det er en tung gjenstand som en stein, er friksjonskraften ubetydelig sammenlignet med vekten av steinen, og dens bane nærmer seg en parabel.
b) Formen på den kastede gjenstanden er også relevant. Hvis et papirark kastes i form av et fly, vil ikke bevegelsen være fritt fall eller parabolsk, siden formen favoriserer luftmotstand.
På den annen side, hvis det samme arket komprimeres til en ball, er den resulterende bevegelsen veldig lik en parabel.
Et prosjektil lanseres fra den horisontale bakken med en hastighet på 10 m / s og en vinkel på 60º. Dette er de samme dataene som figur 1 ble utdypet med. Finn med disse dataene:
a) Øyeblikk der den når maksimal høyde.
b) Maksimal høyde.
c) Hastighet i maksimal høyde.
d) Posisjon og hastighet ved 1,6 s.
e) Øyeblikket det treffer bakken igjen.
f) Den horisontale rekkevidden.
Den vertikale hastigheten som en funksjon av tiden er
vY(t) = vHei - g t = veller sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
I det øyeblikket den maksimale høyden er nådd, er den vertikale hastigheten null et øyeblikk.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Maksimal høyde er gitt av koordinaten Y for øyeblikket hvor høyden er nådd:
og (0,88s) = Jeg + går t -½ g t ^to = 0 + 8,66 * 0,88-½ 9,8 0,88 ^to =
3,83 moh
Derfor er maksimal høyde 3,83 m.
Hastigheten i maksimal høyde er vannrett:
vx(t) = vokse = veller cosθ = 10 cos60º = 5 m / s
Stillingen ved 1,6 s er:
x (1,6) = 5 * 1,6 = 8,0 m
og (1.6) = 8,66 * 1,6-½ 9,8 1,6to = 1,31 m
Når y-koordinaten berører bakken, så:
y (t) = 8,66 * t-½ 9,8 tto = 0 ⇒ t = 1,77 s
Den horisontale rekkevidden er x-koordinaten akkurat i det øyeblikket den berører bakken:
x (1,77) = 5 * 1,77 = 8,85 m
Finn ligningen til banen med dataene fra eksempel 2.
Den parametriske ligningen til banen er:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^to
Og den kartesiske ligningen oppnås ved å løse t fra den første og erstatte den andre
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^to
Forenkling:
y = 1,73 x - 0,20 x ^ 2
Ingen har kommentert denne artikkelen ennå.