Vertikale skuddformler, ligninger, eksempler

De vertikalt skudd Det er en bevegelse som foregår under påvirkning av et kraftfelt, ofte tyngdekraften, og som kan være stigende eller synkende. Det er også kjent under navnet vertikal lansering.

Det mest umiddelbare eksemplet er å kaste opp (eller ned hvis du foretrekker det) en ball med hånden din, selvfølgelig, og sørg for å gjøre den i vertikal retning. Bortsett fra luftmotstand, passer bevegelsen som ballen følger perfekt til Uniformly Varied Rectilinear Motion (MRUV) -modellen..

Det vertikale skuddet er en bevegelse som er mye studert i innledende fysikkurs, da det er et utvalg av bevegelse i en dimensjon, en veldig enkel og nyttig modell.

Denne modellen kan ikke bare brukes til å studere kinematikken til gjenstander under tyngdekraftens virkning, men beskriver også, som det vil sees senere, bevegelsen av partikler midt i et jevnt elektrisk felt..

Artikkelindeks

• 1 Formler og ligninger
  • 1.1 Vertikale kastligninger
• 2 Eksempler
  • 2.1 Arbeidet eksempel 1
  • 2.2 Arbeidet eksempel 2
• 3 Referanser

Formler og ligninger

Det første som trengs er et koordinatsystem for å indikere opprinnelsen og merke det med en bokstav, som i tilfelle vertikale bevegelser er bokstaven "Y".

Deretter velges den positive retningen +Y, som vanligvis er oppover og sansen -Y som vanligvis tas ned (se figur 2). Alt dette med mindre problemløseren bestemmer noe annet, siden et annet alternativ er å ta retning av bevegelsen som positiv, uansett hva den måtte være..

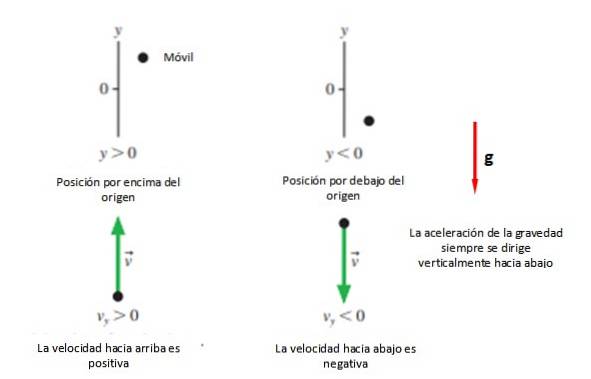
I alle fall anbefales det at opprinnelsen sammenfaller med startpunktet. Y_eller, fordi på denne måten er ligningene forenklet, selv om du kan ta hvilken som helst posisjon du vil begynne å studere bevegelsen.

Vertikale kastligninger

Når vi har etablert koordinatsystemet og opprinnelsen, går vi til ligningene. Størrelsene som beskriver bevegelsen er:

-Starthastighet v_eller

-Akselerasjon til

-Hastighet v

-Start posisjon x_eller

-Posisjon x

-Forskyvning Dx

-Vær t

Alt unntatt tid er vektorer, men siden det er en endimensjonal bevegelse med en viss retning, er det som betyr noe da å bruke + eller - tegn for å indikere hvor størrelsen det er snakk om. Når det gjelder vertikalt trekk, går tyngdekraften alltid nedover, og med mindre annet er angitt, tildeles det et tegn -.

Følgende er ligningene tilpasset vertikal trekk, og erstatter “x"for"Y"Y"til"for"g”. I tillegg inkluderes tegnet (-) som tilsvarer tyngdekraften rettet nedover med en gang:

1) Posisjon: y = y_eller + v_eller.t - ½ g.t^to

2) Hastighet: v = v_eller - g.t

3) Hastighet som en funksjon av forskyvning ΔY: v^to = v_eller^to - 2 g. ΔY

Eksempler

Nedenfor er brukseksempler for vertikal fotografering. I resolusjonen må følgende tas i betraktning:

-"g”Har en konstant verdi som i gjennomsnitt er 9,8 m / s^to eller ca 10 m / s^to hvis det foretrekkes å legge til rette for beregninger når det ikke kreves for mye presisjon.

-Når v_eller greit 0, disse ligningene reduseres til de av fritt fall.

-Hvis lanseringen er oppover, må objektet ha en innledende hastighet som gjør at den kan bevege seg. Når den er i bevegelse, når objektet en maksimal høyde som vil avhenge av hvor stor utgangshastigheten er. Jo høyere høyde, jo mer tid vil mobilen selvfølgelig bruke i luften.

-Objektet går tilbake til startpunktet med samme hastighet som det ble kastet med, men hastigheten er rettet nedover.

-For en vertikal lansering nedover, jo høyere starthastighet, jo raskere vil objektet treffe bakken. Her innstilles den tilbakelagte avstanden i henhold til høyden som er valgt for lanseringen.

-I det vertikale oppoverkastet beregnes tiden det tar for mobilen å nå maksimal høyde v = 0 i ligning 2) i forrige avsnitt. Dette er maksimal tid t_maks:

0 = v_eller - g. t_maks ⇒ t_maks = v_eller / g

-De maksimal høyde Y_maks fjernes fra ligning 3) i forrige avsnitt ved å gjøre det samme v = 0:

0 = v_eller^to - 2 g. Δy ⇒ 0 = v_eller^to - 2 g. (Y_maks - Y_eller) ⇒ og_maks = og_eller  + v_eller^to / 2 g

Ja Y_eller = 0, Det er redusert til:

Y_maks = v_eller^to / 2 g

Arbeidet eksempel 1

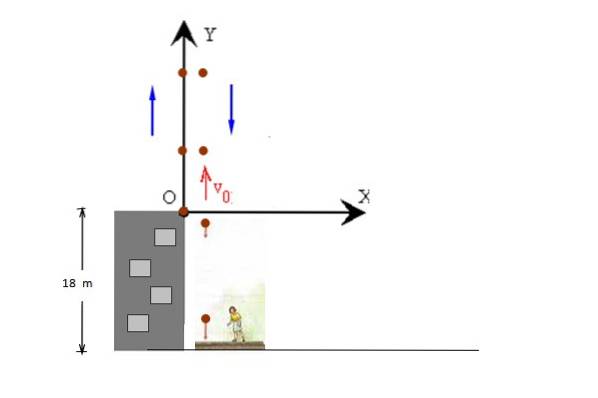
En ball kastes loddrett oppover med v_eller = 14 m / s, fra toppen av en 18 m høy bygning. Ballen får fortsette seg ned til fortauet. Regne ut:

a) Maksimal høyde nådd av ballen i forhold til bakken.

b) Tiden det var i luften (Flytid).

Løsning

Figuren viser løfte- og senkebevegelsene til ballen separat for klarhet, men begge skjer langs samme linje. Utgangsposisjonen tas ved y = 0, slik at den endelige posisjonen er y = - 18 m.

a) Maksimal høyde målt fra taket på bygningen er Y_maks = v_eller^to / 2 g og fra uttalelsen kan vi lese at starthastigheten er +14 m / s, så:

Y_maks = (14 m / s)^to / 2 x 9,8 m / s^to = 10 m (Når det gjelder taket)

H_maks = 10 m + 18 m = 28 m (Angående fortauet).

b) For å finne Total tid eller Flytid ballen holder seg i lufta, ligningen vil bli brukt y = y_eller + v_eller.t - ½ g.t^to, med følgende verdier og tegn:

y = - 18 m

Y_eller = 0 m

v_eller = +14 m / s

Erstatter:

- 18 = 14.t - ½ 9.8 .t^to

- 4,9 t^to+14.t + 18 = 0 

4,9 t^to-14.t - 18 = 0

Det er en ligning av andre grad som lett løses ved hjelp av en vitenskapelig kalkulator eller ved hjelp av løseren. Løsningene er: 3.82 og -0.96. Den negative løsningen kastes siden den mangler fysisk forstand siden den er en tid.

Flytid på ballen er 3,82 sekunder.

Arbeidet eksempel 2

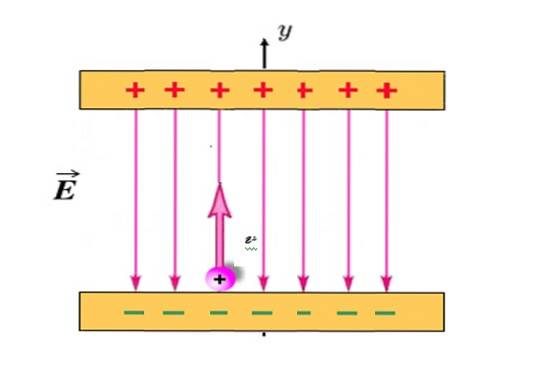
En positivt ladet partikkel med q = +1,2 millicoulombs (mC) og masse m = 2,3 x 10 ^-10 Kg projiseres vertikalt oppover, fra posisjonen vist på figuren og med utgangshastighet v_eller = 30 km / s.

Mellom de ladede platene er det et elektrisk felt OG uniform, rettet vertikalt nedover og med styrke 780 N / C. Hvis avstanden mellom platene er 18 cm, vil partikkelen kollidere med topplaten? Forsøm tyngdekraften på partikkelen, siden den er ekstremt lett.

Løsning

I dette problemet det elektriske feltet OG er den som produserer en kraft F og den påfølgende akselerasjonen. Å være positivt ladet, blir partikkelen alltid tiltrukket av den nedre platen, men når den projiseres vertikalt oppover, vil den nå en maksimal høyde og deretter gå tilbake til den nedre platen, akkurat som ballen i de foregående eksemplene..

Per definisjon av elektrisk felt:

E = F / q = m.a / q ⇒ a = q.E / m

Du må bruke denne ekvivalensen før du erstatter verdier:

1 mC = 1 x 10^-3 C

Dermed er akselerasjonen:

a = 1,2 x 10^-3 x 780 / 2,3 x 10 ^-10m / s^to = 4,07 x 10⁹ m / s^to

For maksimal høyde brukes formelen fra forrige avsnitt, men i stedet for å bruke “g”Denne akselerasjonsverdien brukes:

Y_maks = v_eller^to / 2a = (30.000 m / s)^to/ 2 x 4,07 x 10⁹ m / s^to = 0,11 m = 11 cm

Den kolliderer ikke med den øvre platen, siden den er 18 cm fra startpunktet, og partikkelen bare når opp 11 cm.

Referanser

1. Kirkpatrick, L. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage læring. 23 - 27.
2. Rex, A. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Red. Bind 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 133 - 149.