
Fourier transformasjonsegenskaper, applikasjoner, eksempler
De Fourier transform er en metode for analytisk tilstrekkelighet orientert mot integrerbare funksjoner som tilhører familien til tintegrert forvandlet. Den består av en omdefinering av funksjoner F (t) når det gjelder Cos (t) og Sen (t).
De trigonometriske identitetene til disse funksjonene, sammen med deres avlednings- og antiderivasjonsegenskaper, tjener til å definere Fourier-transformasjonen gjennom følgende komplekse funksjon:
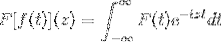
Noe som er sant så lenge uttrykket gir mening, det vil si når den feilaktige integralen er konvergent. Algebraisk sies det at Fourier-transformasjonen er en lineær homeomorfisme.
Hver funksjon som kan arbeides med en Fourier-transform, må presentere null utenfor en definert parameter.
Artikkelindeks
- 1 eiendommer
- 1.1 Eksistens
- 1.2 Lineæriteten til Fourier-transformasjonen
- 1.3 Fouriertransformasjon av et derivat
- 1.4 Differensiering av Fourier-transformasjonen
- 1.5 Fouriertransformasjon av en oversettelse
- 1.6 Oversettelse av Fourier-transformasjonen
- 1.7 Fouriertransformasjon av en skala gruppe
- 1.8 Symmetri
- 1.9 Fouriertransformasjon av et konvolusjonsprodukt
- 1.10 Kontinuitet og forfall til uendelig
- 2 Historie
- 3 Hva er Fourier-transformasjonen til?
- 3.1 Fourier-serien
- 3.2 Andre former for Fourier-serien
- 4 Søknader
- 4.1 Beregning av grunnleggende løsning
- 4.2 Signalteori
- 5 eksempler
- 5.1 Eksempel 1
- 5.2 Eksempel 2
- 6 Forslag til øvelser
- 7 Referanser
Eiendommer

Fourier-transformasjonen oppfyller følgende egenskaper:
Eksistens
For å verifisere eksistensen av Fourier-transformasjonen i en funksjon f (t) definert i realene R, følgende to aksiomer må oppfylles:
- f (t) er stykkevis kontinuerlig for alt R
- f (t) er integrerbar i R
Fourier transformasjonslinearitet
La M (t) og N (t) være to funksjoner med bestemte Fourier-transformasjoner, med alle konstanter a og b.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Som også støttes av lineariteten til integralen med samme navn.
Fourier-transformasjon av et derivat
Den har en funksjon F som er kontinuerlig og integrerbar i alle realene, der:
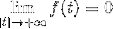
Og derivatet av f (f ') er kontinuerlig og definert stykkevis gjennom R
Fourier-transformasjonen av et derivat er definert av integrering av deler, ved følgende uttrykk:
F [f '(t)] (z) = izF [f (t)] (z)
I høyere ordens avledninger vil den bli brukt på en homolog måte, hvor vi for alle n 1 har:
F [f n'(t)] (z) = (iz)nF [f (t)] (z)
Fourier transformasjon differensiering
Den har en funksjon F som er kontinuerlig og integrerbar i alle realene, der:
i (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Fourier-transformasjon av en oversettelse
For alle θ som tilhører et sett S og T som tilhører settet S ', har vi:
F [ τtil θ] = og-iay F [ θ] F [ τtilT ] = og-iax F [ T]
Med τtil arbeider som oversetteroperatør på vektoren a.
Oversettelse av Fourier-transformasjonen
For alle θ som tilhører et sett S og T som tilhører settet S ', har vi:
τtil F [θ] = F [og-iax.θ] τtil F [T ] = F [og-iay . T]
For alle til som tilhører R
Fourier transform av en skala gruppe
For alle θ som tilhører et sett S. T som tilhører settet S '
λ tilhører R - 0 du må:
F [θ (λx)] = (1 / | λ |) F [θ] (Y /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / λ)
Ja F er en kontinuerlig og tydelig integrerbar funksjon, der a> 0. Deretter:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
For å demonstrere dette resultatet kan vi fortsette med endringen av variabelen.
Når T → + så er s = ved → + ∞
Når T → - så er s = ved → - ∞
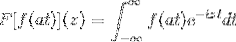
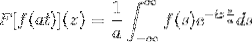
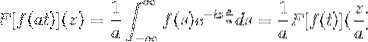
Symmetri
For å studere symmetrien til Fourier-transformasjonen, må identiteten til Parseval og Plancherel-formelen verifiseres.
Vi har θ og δ som tilhører S. Derfra kan det trekkes ut at:
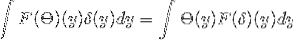
Får
1 / (2π)d F [θ ], F [δ] Parsevals identitet
1 / (2π)d / 2 || F [θ ] ||LtoRd Plancherel formel
Fouriertransformasjon av et konvolusjonsprodukt
Forfølger lignende mål som i Laplace-transformasjonen, refererer sammensmelting av funksjoner til produktet mellom Fourier-transformasjonene.
Vi har f og g som to avgrensede, bestemte og helt integrerbare funksjoner:
F (f * g) = F (f). F (g)
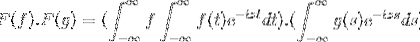
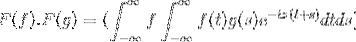
Så når du endrer variabelen
t + s = x; det fortsetter med den feilaktige doble integralen
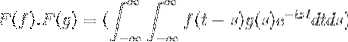
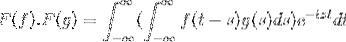
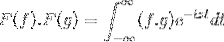
F (f). F (g) = F (f. G)
Kontinuitet og fall i uendelig
For alle θ som tilhører R, F [ θ] overholder kriteriene for en kontinuerlig funksjon avgrenset i Rd.
Også F [ θ] (y) → 0 i C hvis | y | → ∞
Historie
Dette matematiske konseptet ble presentert av Joseph B. Fourier i 1811 mens han utviklet en avhandling om varmespredning. Den ble raskt adoptert av forskjellige grener av vitenskap og ingeniørfag.
Det ble etablert som det viktigste arbeidsverktøyet i studiet av ligninger med delvis derivater, til og med å sammenligne det med det eksisterende arbeidsforholdet mellom Laplace-transformasjon og vanlige differensiallikninger.
Hva er Fourier-transformasjonen til?
Det tjener primært til å forenkle ligninger betydelig, mens transformere avledede uttrykk til kraftelementer, som betegner differensialuttrykk i form av integrerbare polynomer..
I optimalisering, modulering og modellering av resultater fungerer det som et standardisert uttrykk, og er en hyppig ressurs for engineering etter flere generasjoner.
Fourier-serien
De er serier definert i form av Cosines og Sines; De tjener til å lette arbeidet med generelle periodiske funksjoner. Når de brukes, er de en del av teknikkene for å løse vanlige og delvise differensialligninger..
Fourier-serien er enda mer generell enn Taylor-serien, fordi de utvikler periodiske diskontinuerlige funksjoner som ikke har en Taylor-serierepresentasjon..
Andre former for Fourier-serien
For å forstå Fourier-transformasjonen analytisk, er det viktig å gjennomgå de andre måtene Fourier-serien kan bli funnet på, til vi kan definere Fourier-serien i dens komplekse notasjon..
-Fourier-serier på en 2L periodefunksjon
Mange ganger er det nødvendig å tilpasse strukturen til en Fourier-serie til periodiske funksjoner hvis periode er p = 2L> 0 i intervallet [-L, L].
-Fourier-serier i rare og jevne funksjoner
Intervallet [-π, π] blir vurdert, noe som gir fordeler når man utnytter de symmetriske egenskapene til funksjonene.
Hvis f er jevn, er Fourier-serien etablert som en serie Cosines.
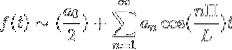
Hvis f er merkelig, blir Fourier-serien etablert som en serie Sines.
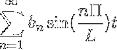
-Kompleks notasjon av Fourier-serien
Hvis vi har en funksjon f (t), som oppfyller alle kravene til utviklingsevne i Fourier-serien, er det mulig å betegne den i intervallet [-t, t] ved å bruke den komplekse notasjonen:
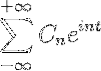
applikasjoner

Beregning av den grunnleggende løsningen
Fourier-transformasjonen er et kraftig verktøy i studien av partielle differensiallikninger av den lineære typen med konstante koeffisienter. De gjelder for funksjoner med ubegrensede domener likt.
I likhet med Laplace-transformasjonen forvandler Fourier-transformasjonen en delvis avledet funksjon til en vanlig differensialligning som er mye enklere å betjene..
Cauchy-problemet for varmeligningen presenterer et felt med hyppig anvendelse av Fourier-transformasjonen der funksjonen genereres varmekjerne eller Dirichlet-kjerne.
Når det gjelder beregningen av den grunnleggende løsningen presenteres følgende tilfeller der det er vanlig å finne Fourier-transformasjonen:
-Laplace-ligning
-Varmeligning
-Schrödinger ligning
-Bølge ligning
Signalteori
Den generelle årsaken til anvendelsen av Fourier-transformasjonen i denne grenen skyldes hovedsakelig den karakteristiske nedbrytningen av et signal som en uendelig overstilling av lettere behandlingsbare signaler.
Det kan være en lydbølge eller en elektromagnetisk bølge, Fourier-transformasjonen uttrykker den i en superposisjon av enkle bølger. Denne representasjonen er ganske hyppig innen elektroteknikk.
På den annen side er det eksempler på anvendelse av Fourier-transformasjonen innen signalteori:
-Problemer med systemidentifikasjon. Etablert f og g
-Konsistensproblem med utgangssignal
-Problemer med signalfiltrering
Eksempler
Eksempel 1
Definer Fourier-transformasjonen for følgende uttrykk:
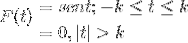
Vi kan også representere det på følgende måte:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
Den rektangulære pulsen er definert:
p (t) = H(t + k) - H(t - k)
Fourier-transformasjonen blir brukt på følgende uttrykk som ligner modulasjonssatsen.
f (t) = p (t) Sen (t)
Hvor: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Og Fourier-transformasjonen er definert av:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Eksempel 2
Definer Fourier-transformasjonen for uttrykket:
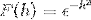
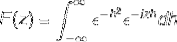
Siden f (h) er en jevn funksjon, kan det fastslås at
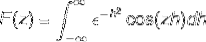
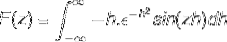
Integrering av deler brukes ved å velge variablene og deres differensialer som følger
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)to v = (e-h)to / to
Erstatte du har
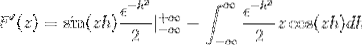
Etter å ha evaluert under den grunnleggende setningen til kalkulus
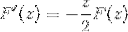
Ved å anvende forkunnskaper om førsteordens differensiallikninger, betegnes uttrykket som
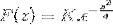
For å få K vurderer vi
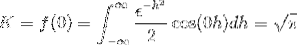
Til slutt er Fourier-transformasjonen av uttrykket definert som
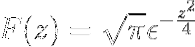
Foreslåtte øvelser
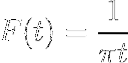
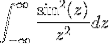
- Få transformasjonen av uttrykket W / (1 + wto)
Referanser
- Duoandikoetxea Zuazo, J., Fourier analyse. Addison- Wesley Iberoamericana, Autonomous University of Madrid, 1995.
- Lions, J. L., matematisk analyse og numeriske metoder for vitenskap og teknologi. Springer-Verlag, 1990.
- Lieb, E. H., Gaussiske kjerner har bare gaussiske maksimeringsmidler. Finne opp. Matte. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier Series and Integrals. Academic Press, New York, 1972.
- Schwartz, L., Théorie des Distributions. Ed. Hermann, Paris, 1966.



Ingen har kommentert denne artikkelen ennå.