
Diskrete Fourier-transformasjonsegenskaper, applikasjoner, eksempler
De diskret Fourier-transform er en numerisk metode som brukes til å definere prøver som refererer til spektralfrekvensene som utgjør et signal. Studer periodiske funksjoner i lukkede parametere, og gir et annet diskret signal.
For å oppnå den diskrete Fourier-transformasjonen av N-punkter, på et diskret signal, må følgende 2 betingelser oppfylles i en sekvens x [n]
x [n] = 0 n < 0 ˄ n > N - 1
Hvis disse forholdene er oppfylt, kan den diskrete Fourier-transformasjonen defineres som
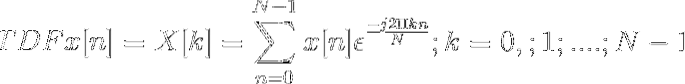
Den diskrete Fourier-transformasjonen kan defineres som et N-punkt utvalg av Fourier-transformasjonen.
Artikkelindeks
- 1 Tolkning av den diskrete Fourier-transformasjonen
- 2 eiendommer
- 2.1 Linearitet
- 2.2 Dualitet
- 2.3 Konvolusjon
- 2.4 Rulling
- 2.5 Konjugat symmetri
- 2.6 Modulering
- 2.7 Produkt
- 2.8 Symmetri
- 2.9 Konjugat
- 2.10 Parseval ligning
- 3 Likheter og forskjeller med Fourier-transformasjonen
- 4 Hva er den diskrete Fourier-transformasjonen til?
- 5 Historie
- 6 Diskret Fourier-transformasjon og dens inverse
- 7 vinget
- 8 Søknader
- 8.1 Beregning av grunnleggende løsning
- 8.2 Signalteori
- 9 Fourier-serien
- 10 Andre former for Fourier-serien
- 11 Eksempler
- 12 Øvelser
- 12.1 Øvelse 1
- 12.2 Øvelse 2
- 13 Referanser
Tolkning av den diskrete Fourier-transformasjonen

Det er to synsvinkler som resultatene fra en sekvens x kan tolkes fras[n] gjennom den diskrete Fourier-transformasjonen.
-Den første tilsvarer spektralkoeffisientene, som allerede er kjent fra Fourier-serien. Det observeres i diskrete periodiske signaler, med prøver som sammenfaller med sekvensen xs[n].
-Den andre omhandler spekteret av et diskret aperiodisk signal, med prøver som tilsvarer sekvensen xs[n].
Den diskrete transformasjonen er en tilnærming til spekteret til det originale analoge signalet. Fasen avhenger av prøvetakingsøyeblikkene, mens størrelsen avhenger av prøvetakingsintervallet..
Eiendommer
De algebraiske fundamentene til strukturen utgjør de logiske grunnlagene i de følgende avsnittene.
Lineæritet
C. Sn → C. F [Sk]; Hvis en sekvens multipliseres med en skalar, vil dens transformasjon også være.
Tn + Vn = F [Tk] + F [Vk]; Transformasjonen av en sum er lik summen av transformasjonene.
Dualitet
F [Sn] → (1 / N) S-k; Hvis den diskrete Fourier-transformen beregnes på nytt til et allerede transformert uttrykk, oppnås det samme uttrykket, skalert i N og invertert i forhold til den vertikale aksen.
Konvolusjon
Forfølger lignende mål som i Laplace-transformasjonen, refererer sammensmelting av funksjoner til produktet mellom deres Fourier-transformasjoner. Konvolusjon gjelder også diskrete tider og er ansvarlig for mange moderne prosedyrer..
Xn * Rn → F [Xn] .F [Rn]; Transformasjonen av en konvolusjon er lik produktet av transformasjonene.
Xn . Rn→ F [Xn] * F [Rn]; Transformeringen av et produkt er lik transformasjonen av transformasjonen.
Forskyvning
Xn-m → F [Xk] e -i (2π / N) km ; Hvis en sekvens er forsinket i m prøver, vil dens effekt på den diskrete transformasjonen være en modifikasjon av vinkelen definert av (2π / N) km.
Symmetri konjugert
Xt [-k] = X *t[k] = Xt [N - K]
Modulering
W-nmN . x [n] ↔ Xt[k - m]
Produkt
x [n] y [n] ↔ (1 / N) Xt[k] * Yt[k]
Symmetri
X [-n] ↔ Xt[-k] = X *t[k]
Konjugert
x * [n] ↔ X *t[-k]
Parseval ligning
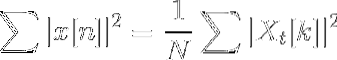
Likheter og forskjeller med Fourier-transformasjonen
Når det gjelder den konvensjonelle Fourier-transformasjonen, har den flere likheter og forskjeller. Fourier-transformasjonen konverterer en sekvens til en hel linje. På denne måten sies det at resultatet av Fourier-variabelen er en kompleks funksjon av en reell variabel.
Den diskrete Fourier-transformasjonen mottar, i motsetning til, et diskret signal og transformerer det til et annet diskret signal, det vil si en sekvens.
Hva er den diskrete Fourier-transformasjonen for?
De tjener primært til å forenkle ligninger betydelig, mens de transformerer avledede uttrykk til kraftelementer. Betegner differensialuttrykk i form av integrerbare polynomer.
I optimalisering, modulering og modellering av resultater fungerer det som et standardisert uttrykk, og er en hyppig ressurs for engineering etter flere generasjoner.
Historie
Dette matematiske konseptet ble presentert av Joseph B. Fourier i 1811, mens han utviklet en avhandling om varmespredning. Den ble raskt adoptert av forskjellige grener av vitenskap og ingeniørfag.
Det ble etablert som det viktigste arbeidsverktøyet i studiet av ligninger med delvis derivater, til og med å sammenligne det med det eksisterende arbeidsforholdet mellom Laplace-transformasjon og vanlige differensiallikninger.
Hver funksjon som kan arbeides med en Fourier-transform, må presentere null utenfor en definert parameter.
Diskret Fourier-transformasjon og dens inverse
Den diskrete transformasjonen oppnås gjennom uttrykket:
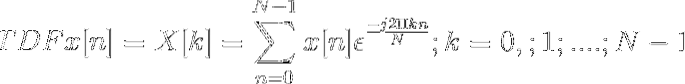
Etter å ha gitt en diskret sekvens X [n]
Det omvendte av den diskrete Fourier-transformasjonen er definert gjennom uttrykket:
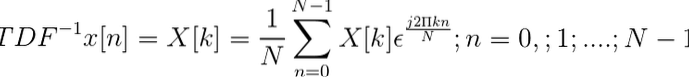
Når den diskrete transformasjonen er oppnådd, tillater den å definere sekvensen i tidsdomenet X [n].
Bevinget
Parametriseringsprosessen som tilsvarer den diskrete Fourier-transformasjonen ligger i vinduet. For å utføre transformasjonen må vi begrense sekvensen i tid. I mange tilfeller har ikke de aktuelle signalene disse begrensningene.
En sekvens som ikke oppfyller størrelseskriteriene som skal gjelde for den diskrete transformasjonen, kan multipliseres med en "vindu" -funksjon V [n], som definerer oppførselen til sekvensen i en kontrollert parameter.
X [n]. V [n]
Spektrumbredden vil avhenge av vinduets bredde. Når bredden på vinduet øker, vil den beregnede transformasjonen bli smalere.
applikasjoner
Beregning av den grunnleggende løsningen
Den diskrete Fourier-transformasjonen er et kraftig verktøy i studiet av diskrete sekvenser.
Den diskrete Fourier-transformasjonen forvandler en kontinuerlig variabel funksjon, til en diskret variabel transformasjon.
Cauchy-problemet for varmeligningen presenterer et hyppig anvendelsesfelt for den diskrete Fourier-transformasjonen. Hvor funksjonen genereres varmekjerne eller Dirichlet-kjerne, som gjelder prøvetaking av verdier i en definert parameter.
Signalteori
Den generelle årsaken til anvendelsen av den diskrete Fourier-transformasjonen i denne grenen skyldes hovedsakelig den karakteristiske nedbrytningen av et signal som en uendelig superposisjon av lettere behandlingsbare signaler.
Det kan være en lydbølge eller en elektromagnetisk bølge, den diskrete Fourier-transformasjonen uttrykker den i en superposisjon av enkle bølger. Denne representasjonen er ganske hyppig innen elektroteknikk.
Fourier-serien
De er serier definert i form av Cosines og Sines. De tjener til å lette arbeidet med generelle periodiske funksjoner. Når de brukes, er de en del av teknikkene for å løse vanlige og delvise differensialligninger..
Fourier-serien er enda mer generell enn Taylor-serien, fordi de utvikler periodiske diskontinuerlige funksjoner som ikke har en Taylor-serierepresentasjon..
Andre former for Fourier-serien
For å forstå Fourier-transformasjonen analytisk, er det viktig å gjennomgå de andre måtene Fourier-serien kan bli funnet, til vi kan definere Fourier-serien i den komplekse notasjonen..
-Fourier-serien på en 2L periode-funksjon:
Mange ganger er det nødvendig å tilpasse strukturen til en Fourier-serie til periodiske funksjoner hvis periode er p = 2L> 0 i intervallet [-L, L].
-Fourier-serier i rare og jevne funksjoner
Intervallet [-π, π] blir vurdert, noe som gir fordeler når man utnytter de symmetriske egenskapene til funksjonene.
Hvis f er jevn, er Fourier-serien etablert som en serie Cosines.
Hvis f er merkelig, blir Fourier-serien etablert som en serie Sines.
-Kompleks notasjon av Fourier-serien
Hvis vi har en funksjon f (t), som oppfyller alle kravene i Fourier-serien, er det mulig å betegne den i intervallet [-t, t] ved å bruke den komplekse notasjonen:
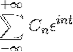
Eksempler
Når det gjelder beregning av den grunnleggende løsningen presenteres følgende eksempler:
Laplace-ligning
Varmeligning
Schrödinger ligning
Bølge ligning
På den annen side er følgende eksempler på anvendelse av den diskrete Fourier-transformasjonen innen signalteorien:
-Problemer med systemidentifikasjon. Etablert f og g
-Konsistensproblem med utgangssignal
-Problemer med signalfiltrering
Opplæring
Øvelse 1
Beregn den diskrete Fourier-transformasjonen for følgende sekvens.
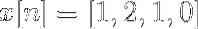
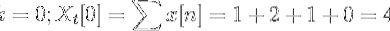
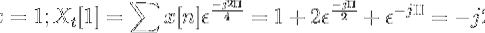
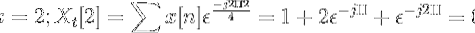
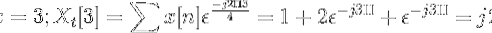
Du kan definere kraftuttaket til x [n] som:
Xt[k] = 4, -j2, 0, j2 for k = 0, 1, 2, 3
Øvelse 2
Vi ønsker å bestemme spektral signalet definert av uttrykket x (t) = e gjennom en digital algoritme-t. Der hvor maksimal frekvens som ber om koeffisient er fm= 1Hz. En harmonisk tilsvarer f = 0,3 Hz. Feilen er begrenset til mindre enn 5%. Regne ut Fs , D og N.
Tar vi hensyn til prøvetakingssetningen Fs = 2fm = 2 Hz
En frekvensoppløsning på F0 = 0,1 Hz, hvorfra du får D = 1 / 0,1 = 10s
0,3 Hz er frekvensen som tilsvarer indeksen k = 3, der N = 3 × 8 = 24 prøver. Angir at Fs = Ikke relevant = 24/10 = 2,4> 2
Siden målet er å få lavest mulig verdi for N, kan følgende verdier betraktes som en løsning:
F0 = 0,3 Hz
D = 1 / 0,3 = 3,33 s
k = 1
N = 1 × 8 = 8
Referanser
- Mestring av den diskrete Fourier-transformasjonen i en, to eller flere dimensjoner: fallgruver og gjenstander. Isaac Amidror. Springer Science & Business Media, 19. juli. 2013
- DFT: En eierhåndbok for diskret Fourier-transformasjon. William L. Briggs, Van Emden Henson. SIAM, 1. jan. nitten nitti fem
- Digital signalbehandling: Teori og praksis. D. Sundararajan. World Scientific, 2003
- Transformasjoner og raske algoritmer for signalanalyse og representasjoner. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. des. 2012
- Diskrete og kontinuerlige Fourier-transformasjoner: analyse, applikasjoner og raske algoritmer. Eleanor Chu. CRC Press, 19. mars. 2008


Ingen har kommentert denne artikkelen ennå.