
Historie trekanter, elementer, klassifisering, egenskaper

De trekanter De er flate og lukkede geometriske figurer, bestående av tre sider. En trekant bestemmes av tre linjer som krysser hverandre to og to og danner tre vinkler med hverandre. Den trekantede formen, full av symbolikk, er til stede i utallige gjenstander og som et konstruksjonselement.
Opprinnelsen til trekanten er tapt i historien. Fra arkeologiske bevis er det kjent at den primitive menneskeheten visste det godt, ettersom arkeologiske levninger bekrefter at den ble brukt i verktøy og våpen.

Det er også klart at de gamle egypterne hadde en solid kunnskap om geometri og spesielt om den trekantede formen. De ble reflektert i de arkitektoniske elementene i de monumentale bygningene.
I Rhind er papyrus formler for beregning av arealer av trekanter og trapeser, samt noen volumer og andre begreper om rudimentær trigonometri.
For deres del er det kjent at babylonerne var i stand til å beregne arealet av trekanten og andre geometriske figurer, som de brukte for praktiske formål, for eksempel landdeling. De var også kunnskapsrike om mange egenskaper til trekanter.
Imidlertid var det de gamle grekerne som systematiserte mange av de geometriske begrepene som var vanlige i dag, selv om mye av denne kunnskapen ikke var eksklusiv, siden den sikkert ble delt med disse andre gamle sivilisasjonene..
Artikkelindeks
- 1 Elementer av trekanten
- 1.1 Notasjon
- 2 typer trekanter
- 2.1 Kongruens av trekanter
- 2.2 Likhet mellom trekanter
- 3 eiendommer
- 4 teoremer
- 4.1 Thales første setning
- 4.2 Thales andre setning
- 4.3 Pythagoras teorem
- 5 Området til en trekant
- 6 Eksempler på trekanter
- 6.1 Eksempel 1
- 6.2 Eksempel 2
- 6.3 Eksempel 3
- 7 Øvelser
- 7.1 Øvelse 1
- 7.2 Øvelse 2
- 8 Referanser
Trekantelementer
Elementene i en hvilken som helst trekant er angitt i følgende figur. Det er tre: hjørner, sider og vinkler.
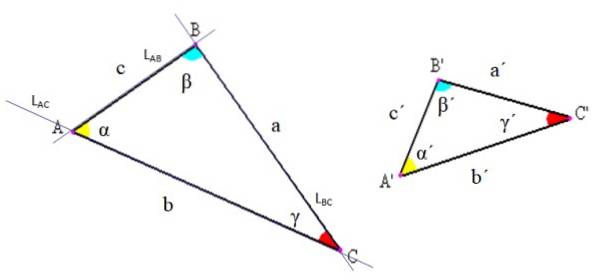
-Hjørner: er skjæringspunktene til linjene hvis segment bestemmer trekanten. I figuren over, for eksempel, linjen LAC som inneholder segment AC, krysser linje LAB som inneholder segment AB akkurat ved punkt A.
-Sider: mellom hvert par av toppunktene tegnes et linjesegment som utgjør den ene siden av trekanten. Dette segmentet kan betegnes med sluttbokstavene eller ved å bruke en bestemt bokstav for å kalle det. I eksemplet i figur 2 kalles side AB også "c".
-Vinkler: Mellom hver side med et felles toppunkt stammer en vinkel, hvis topp faller sammen med trekanten. Vanligvis er vinkelen betegnet med en gresk bokstav, som det ble sagt i begynnelsen.
For å bygge en bestemt trekant, med en gitt form og størrelse, har du bare ett av følgende datasett:
-Alle tre sidene, ganske åpenbare for en trekant.
-To sider og vinkelen mellom dem, og umiddelbart trekkes den gjenværende siden.
-To (indre) vinkler og siden mellom dem. I forlengelse tegnes de to manglende sidene og trekanten er klar.
Notasjon
Generelt sett blir følgende konvensjoner brukt i trekantnotasjoner: hjørner er angitt med store bokstaver, sider med små latinske bokstaver og vinkler med greske bokstaver (se figur 2).
På denne måten er trekanten navngitt i henhold til toppunktene. For eksempel er trekanten til venstre i figur 2 trekanten ABC, og den til høyre er trekanten A'B'C '.
Det er også mulig å bruke andre notasjoner; for eksempel er vinkelen α i figur 2 betegnet som BAC. Merk at bokstaven i toppunktet går i midten og bokstavene skrives mot klokken.
Andre ganger plasseres et oppslag for å betegne vinkelen:
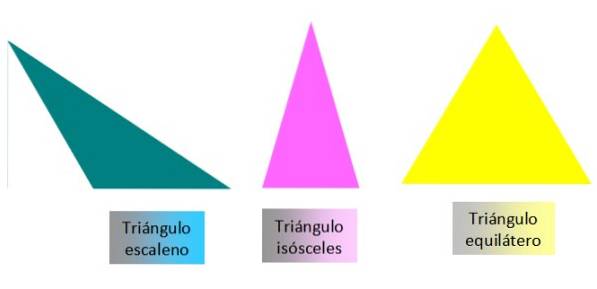
α = ∠A
Typer av trekanter
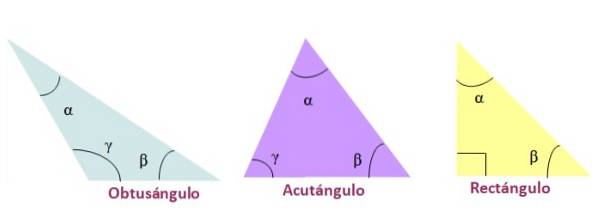
Det er flere kriterier for å klassifisere trekanter. Det vanligste er å klassifisere dem etter målene på sidene eller etter målene på vinklene. Avhengig av mål på sidene, kan trekantene være: skaler, likebenede eller likesidige:
-Scalene: dens tre sider er forskjellige.
-Likebent: har to like sider og en annen side.
-Likesidig: alle tre sidene er like.

I henhold til målene på deres vinkler, blir trekantene navngitt slik:
-Stump vinkel, hvis en av de indre vinklene er større enn 90º.
-Spiss vinkel, når de tre indre vinklene i trekanten er spisse, det vil si mindre enn 90º
-Rektangel, i tilfelle en av dens indre vinkler er 90º. Sidene som danner 90º kalles ben og siden motsatt rett vinkel er hypotenusen..
Kongruens av trekanter
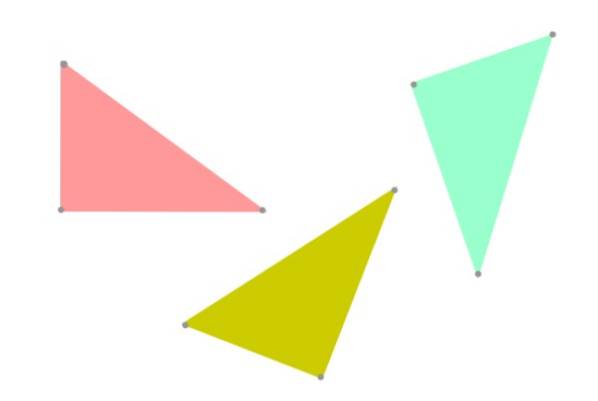
Når to trekanter har samme form og har samme størrelse, sies de å være kongruente. Selvfølgelig er kongruens relatert til likhet, så hvorfor snakker vi i geometri om "to kongruente trekanter" i stedet for "to like trekanter"?
Vel, det er foretrukket å bruke begrepet "kongruens" for å holde fast ved sannheten, siden to trekanter kan ha samme form og størrelse, men være orientert annerledes i planet (se figur 3). Fra geometriens synspunkt ville de ikke lenger være de samme.
Kongruensekriterier
To trekanter er kongruente hvis noe av det følgende skjer:
-Alle tre sidene måler det samme (igjen er dette det mest åpenbare).
-De har to identiske sider og med samme vinkel mellom seg.
-Begge har to identiske indre vinkler, og siden mellom disse vinklene måler det samme.
Som man kan se handler det om at de to trekantene oppfyller de nødvendige forholdene slik at når de er bygget, er formen og størrelsen nøyaktig den samme..
Kongruensekriteriene er veldig nyttige, siden i praksis må utallige deler og mekaniske deler produseres i serie, på en slik måte at deres mål og form er nøyaktig den samme.
Likhet med trekanter
En trekant ligner på en annen hvis de har samme form, selv om de har forskjellige størrelser. For å sikre at formen er den samme, kreves det at de indre vinklene har samme verdi og at sidene er proporsjonale..
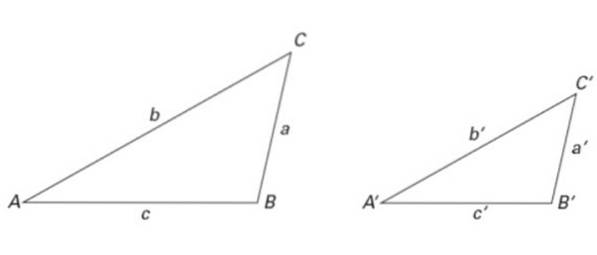
Trekantene i figur 2 er også like, som de er i figur 6. På denne måten:
∠ A = ∠ A ', ∠ B = ∠ B 'og ∠ C = ∠ C '
Når det gjelder sidene, gjelder følgende likhetsforhold:
a / a '= b / b' = c / c '
Eiendommer
De grunnleggende egenskapene til trekanter er som følger:
-Summen av innvendige vinkler i en hvilken som helst trekant er alltid 180º.
-For en hvilken som helst trekant er summen av de utvendige vinklene lik 360 °.
- En ekstern vinkel av en trekant er lik summen av de to indre vinklene som ikke ligger i nærheten av nevnte vinkel.
Setninger
Thales første setning
De tilskrives den greske filosofen og matematikeren Thales of Miletus, som utviklet flere teoremer knyttet til geometri. Den første av dem fastslår følgende:
Hvis flere parallelle linjer skjærer to tverrgående linjer, bestemmes segmenter som er proporsjonale i dem.
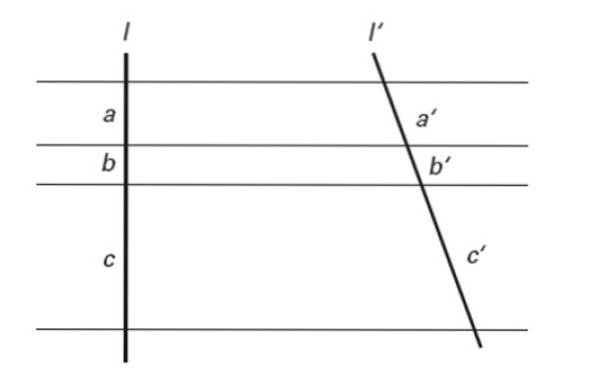
Med andre ord:
a / a '= b / b' = c / c '
Thales første setning gjelder for en trekant, for eksempel har vi den blå trekanten ABC til venstre, som er kuttet av de røde parallellene til høyre:
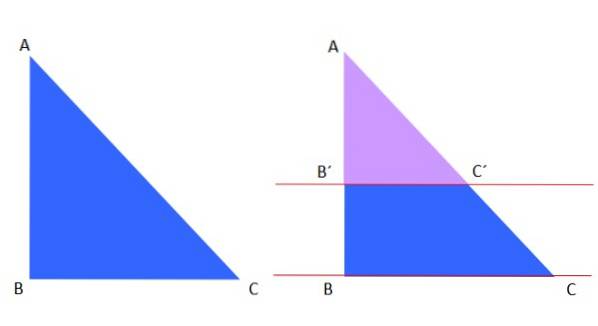
Den fiolette trekanten AB'C 'ligner den blå trekanten ABC, ifølge Thales' teorem kan følgende skrives:
AB '/ AC' = AB / AC
Og det samsvarer med det som ble forklart tidligere i segmentet av likheten mellom trekanter. For øvrig kan parallelle linjer også være vertikale eller parallelle med hypotenusen, og lignende trekanter oppnås på samme måte.
Thales 'andre setning
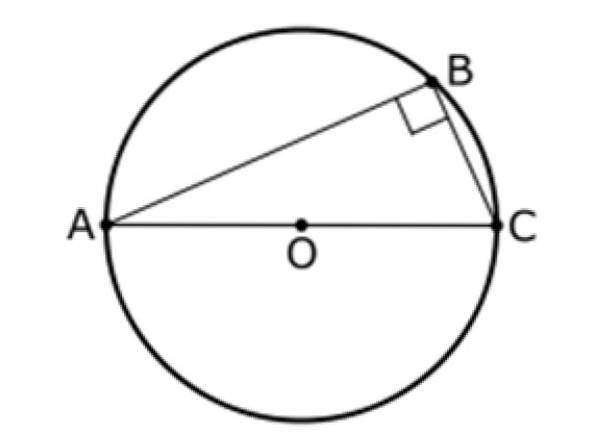
Denne setningen refererer også til en trekant og en sirkel med sentrum O, som de som er vist nedenfor. I denne figuren er AC en diameter på omkretsen og B er et punkt på den, B er forskjellig fra A og B.
Thales 'andre setning sier at:
Vinkelen mellom segmentene AB og BC er alltid 90º, derfor er trekanten ABC riktig.
Pythagoras teorem
Dette er en av de mest berømte setningene i historien. Det skyldes den greske matematikeren Pythagoras fra Samos (569 - 475 f.Kr.) og kan brukes i en rett trekant. Sier slik:
Summen av kvadratene til lengden på bena til høyre trekant er lik lengden på hypotenusen i kvadrat.
Hvis vi tar et eksempel på den blå trekanten i figur 8, eller den fiolette trekanten, siden begge er rektangler, kan det sies at:
ACto = ABto + F.Kr.to (blå trekant)
AC 'to = AB 'to + BC 'to (lilla trekant)
Området til en trekant
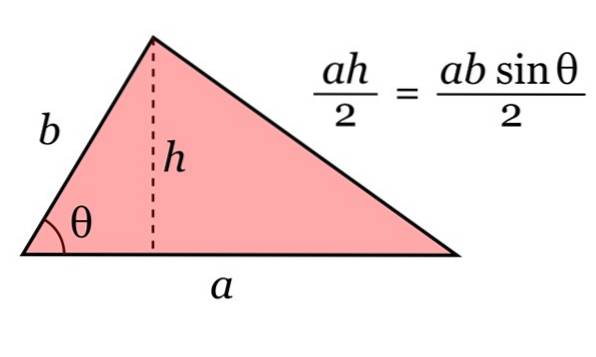
Området av trekanten er gitt av produktet av basen til og høyden din h, delt på 2. Og ved trigonometri kan denne høyden skrives som h = b sinθ.
Eksempler på trekanter
Eksempel 1
Det sies at ved hjelp av sin første teorem klarte Thales å måle høyden på den store pyramiden i Egypt, et av de 7 underverkene i den antikke verden, ved å måle skyggen som den projiserte på bakken og som projiseres av en pæl. kjørt i bakken..
Dette er oversikten over prosedyren fulgt av Tales:
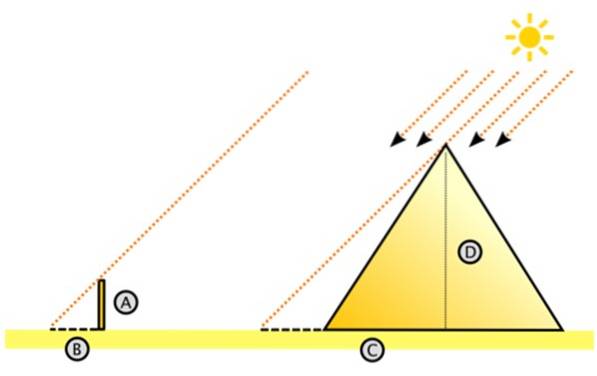
Thales antok riktig at solstrålene treffer parallelt. Med dette i bakhodet så han for seg den store høyre trekanten til høyre.
Der er D pyramidens høyde og C er avstanden over bakken målt fra sentrum til skyggen som pyramiden kastet på ørkenbunnen. Det kan være arbeidskrevende å måle C, men det er absolutt lettere enn å måle høyden på pyramiden.
Til venstre er den lille trekanten, med ben A og B, hvor A er høyden på staven som drives loddrett i bakken og B er skyggen den kaster. Begge lengdene er målbare, og det samme er C (C er lik skyggelengden + halvparten av pyramiden).
Så av likhet med trekanter:
A / B = D / C
Og høyden på den store pyramiden viser seg å være: D = C. (A / B)
Eksempel 2
Takstoler i sivil konstruksjon er strukturer laget av kryss og tvers tynne stenger av tre eller metall, som brukes som støtte i mange bygninger. De er også kjent som gitter, takstoler eller gitter (fagverk på engelsk).
I dem er trekantene alltid til stede, siden stolpene er sammenkoblet på punkter som kalles noder, som kan være faste eller artikulerte..

Eksempel 3
Metoden kjent som triangulering gjør det mulig å oppnå plassering av utilgjengelige punkter, med kunnskap om andre avstander som er lettere å måle, forutsatt at det dannes en trekant som inkluderer ønsket plassering mellom toppunktene..
For eksempel, i den følgende figuren vil vi vite hvor skipet ligger i sjøen, betegnet som B.
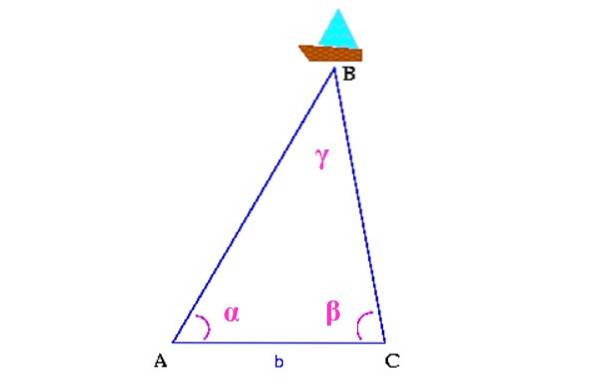
Først måles avstanden mellom to punkter på kysten, som i figuren er A og C. Deretter må vinklene α og β bestemmes, ved hjelp av en teodolitt, en enhet som brukes til å måle vertikale og horisontale vinkler.
Med all denne informasjonen er det bygget en trekant i hvis øvre toppunkt er skipet. Det vil forbli å beregne vinkelen γ, ved hjelp av egenskapene til trekantene og avstandene AB og CB ved hjelp av trigonometri, for å bestemme skipets posisjon i havet.
Opplæring
Øvelse 1
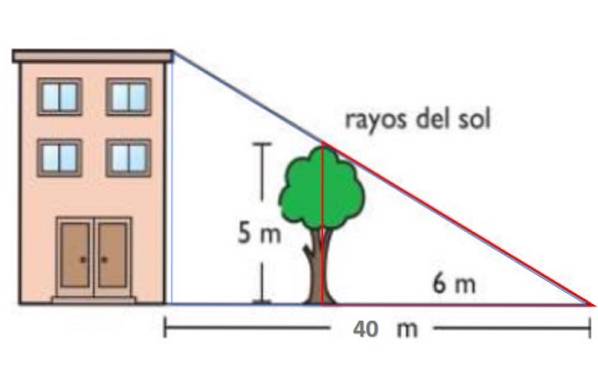
I figuren vist er solstrålene parallelle. På denne måten kaster det 5 meter høye treet en 6 meter skygge på bakken. Samtidig er skyggen av bygningen 40 meter. Følg høyden på bygningen etter Thales 'første sætning.
Løsning
Den røde trekanten har sider på henholdsvis 5 og 6 meter, mens den blå har høyde H - bygningens høyde - og base 40 meter. Begge trekanter er like, derfor:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
Øvelse 2
Du må vite den horisontale avstanden mellom to punkter TIL Y B, men de ligger på et veldig ujevnt underlag.
Om midtpunktet (sm) av dette landet skiller seg ut en fremtredende rolle på 1,75 meter høy. Hvis målebåndet indikerer 26 meter i lengde målt fra A til fremtredende, og 27 meter fra B til samme punkt, finn avstanden AB.
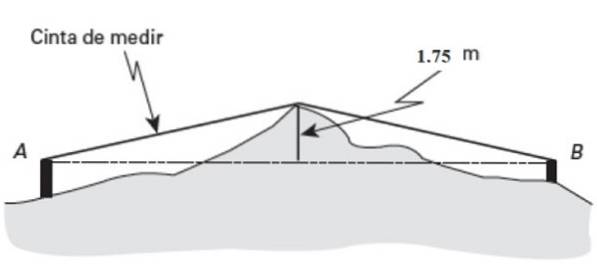
Løsning
Pythagoras-teoremet brukes på en av de to høyre trekantene i figuren. Starter med den til venstre:
Hypotenuse = c = 26 meter
Høyde = a = 1,75 meter
APm = (26to - 1,75to)1/2 = 25,94 m
Påfør nå Pythagoras i trekanten til høyre, denne gangen c = 27 meter, a = 1,75 meter. Med disse verdiene:
BPm= (27to - 1,75to)1/2 = 26,94 m
Avstanden AB blir funnet ved å legge til disse resultatene:
AB = 25,94 m + 26,94 m = 52,88 m.
Referanser
- Baldor, J. A. 1973. Plane and Space Geometry. Mellomamerikansk kultur.
- Barredo, D. Geometrien til trekanten. Gjenopprettet fra: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matematikk II. Geometri og trigonometri. Andre utgave. Pearson.
- Wentworth, G. Plane Geometry. Gjenopprettet fra: gutenberg.org.
- Wikipedia. Triangel. Gjenopprettet fra: es. wikipedia.org.



Ingen har kommentert denne artikkelen ennå.