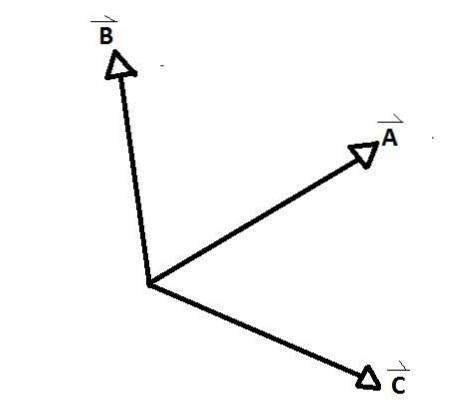
De samtidige vektorer er gruppene av vektorer hvis akser sammenfaller på et punkt og danner mellom hvert par av dem en indre og en ekstern vinkel. Et klart eksempel ses i figuren nedenfor, der A, B og C er vektorer samtidig med hverandre.
D og E i motsetning til resten er ikke. Det er vinkler dannet mellom de samtidige vektorene AB, AC og CB. De kalles forholdsvinkler mellom vektorene.
Artikkelindeks
-De har et felles punkt, som sammenfaller med opprinnelsen: alle størrelsene til de samtidige vektorene starter fra et felles punkt til deres respektive ekstremer..
-Opprinnelsen betraktes som vektorens handlingspunkt: et handlingspunkt må etableres som vil bli direkte påvirket av hver av de samtidige vektorene.
-Hans domene i plan og rom er Rto og R3 henholdsvis: de samtidige vektorene kan fritt dekke hele det geometriske rommet.
-Det tillater forskjellige notasjoner i samme gruppe vektorer. I følge grenene av studien er forskjellige notasjoner til stede i operasjoner med vektorer.
Grenen av vektorer har flere underavdelinger, hvorav noen kan navngis: parallell, vinkelrett, koplanar, tilsvarende, motsatt og enhetlig. Samtidige vektorer er oppført her, og som alle de som er nevnt ovenfor, har de mange applikasjoner innen forskjellige vitenskaper..
De er veldig vanlige i studien av vektorer, fordi de representerer en nyttig generalisering i operasjonene med dem. Både i flyet og i rommet brukes samtidige vektorer ofte til å representere forskjellige elementer og studere deres innflytelse på et bestemt system..
Det er flere måter å representere et vektorelement på. De viktigste og mest kjente er:
Foreslått av den samme matematiske tilnærmingen, betegner den vektorene med en trippel som tilsvarer størrelsen på hver akse (x, y, z)
A: (1, 1, -1) Mellomrom A: (1, 1) Fly
De tjener bare til å betegne vektorer i planet, selv om de i den integrerte kalkulatoren tildeles dybdekomponenten. Den er sammensatt med en lineær størrelse r og en vinkel i forhold til polaraksen Ɵ.
A: (3, 450 Fly A: (2, 450 , 3) Rom
De definerer størrelsen på vektoren ved hjelp av versores. Versores (i + j + k) representerer enhetsvektorene som tilsvarer aksene X, Y Y
A: 3i + 2j - 3k
De ligner på polær notasjon, men med tillegg av en andre vinkel som feier over flyet xy symbolisert av δ.
A: (4, 60eller , π / 4)
Samtidige vektorer brukes mest for å definere operasjoner mellom vektorer, fordi det er lettere å sammenligne elementene i vektorene når de presenteres samtidig..
Summen av samtidige vektorer har som mål å finne den resulterende vektoren Vr. Som ifølge grenen av studien tilsvarer en endelig handling
For eksempel: 3 strenger A, B, C er bundet til en rute, hver ende av strengen holdes av et emne. Hver av de tre fagene må trekke tauet i en annen retning enn de andre 2.
A: (ax, ay, az) B: (bx, by, bz) C: (cx, cy, cz)
A + B + C = (ax + bx + cx; ay + av + cy; az + bz + cz) = Vr
Boksen vil derfor bare kunne bevege seg i en retning Vr vil indikere boksens retning og bevegelsesretning.
Det er mange kriterier angående forskjellen mellom vektorer, mange forfattere velger å ekskludere den og sier at bare summen mellom vektorene er angitt, der forskjellen handler om summen av den motsatte vektoren. Sannheten er at vektorene kan trekkes algebraisk.
A: (øks, ay, az) B: (bx, av, bz)
A - B = A + (-B) = (ax-bx; ay-by; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]
Også kjent som et prikkprodukt, genererer det en skalarverdi som kan relateres til forskjellige størrelser, avhengig av grenen av studien..
For geometri indikerer arealet av parallellogrammet dannet av paret av samtidige vektorer gjennom parallellogrammetoden. For mekanisk fysikk definerer arbeidet utført av en styrke F når du flytter en kropp en avstand Δr.
ѡ = F . Δr
Som navnet antyder, genererer den en skalarverdi og defineres som følger:
La vektorene A og B være
A: (øks, ay, az) B: (bx, av, bz)
-Analytisk form:
(A. B) = | A |. | B | .Cos θ
Hvor θ er den indre vinkelen mellom begge vektorene
-Algebraisk form:
(A. B) = (ax.bx + ay.by + az.bz)
Korsproduktet eller punktproduktet mellom to vektorer definerer en tredje vektor C som har kvaliteten på å være vinkelrett på B Y C. I fysikk definerer du momentvektoren τ basiselement for rotasjonsdynamikk.
-Analytisk form:
| A x B | = | A |. | B | .Sen θ
-Algebraisk form:
(A x B) = = (Ax. By - ay. Bx) - (ax. Bz - az. Bx) j + (aks. av - ay. bx) k
-Relativ bevegelse: rA / B
Relativitetsgrunnlaget er relativ bevegelse og samtidige vektorer er grunnlaget for relativ bevegelse. Relative posisjoner, hastigheter og akselerasjoner kan utledes ved å bruke følgende ideerekkefølge.
r A / B = rTIL - rB ; Relativ stilling til A med hensyn til B
v A / B = vTIL - vB ; Relativ hastighet av A med hensyn til B
til A / B = aTIL - tilB ; Relativ akselerasjon av A med hensyn til B
La A, B og C være samtidige vektorer.
A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)
-Definer den resulterende vektoren Vr = 2A - 3B + C.
2A = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)
-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)
Vr = 2A + (-3B) + C = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)
Vr = ([-2 + (- 9) + (- 4)]; [6 + (- 15) + (- 2)]; (10 + 6 + 1))
Vr = (-15, -11, 17)
-Definer punktproduktet (A.C)
(A. C) = (-1, 3, 5). (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4-6 + 5
(A. C) = 3
-Beregn vinkelen mellom A og C
(A. C) = | A |. | C |. Cos θ Hvor θ er den korteste vinkelen mellom vektorene
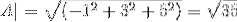
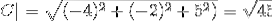
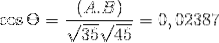
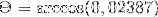
θ = 88,630
-Finn en vektor vinkelrett på A og B
For dette er det nødvendig å definere vektorproduktet mellom (-1, 3, 5) og (3, 5, -2). Som forklart før, er en 3 x 3 matrise konstruert der den første raden er sammensatt av trippel enhetsvektorene (i, j, k). Deretter består 2. og 3. rad av vektorene som skal opereres, med respekt for operasjonsrekkefølgen.
(A x B) = = [(-1). 5 - (3. 3)] Jeg - [ (-1) . (-2) - (5. 3)] j + [ (-1) . 5 - (3. 3)] k
(A x B) = (-5 - 9) Jeg - (2 - 15) j + (-5 - 9) k
(A x B) = -14 I + 13 j - 14 k
La Vtil og Vb hastighetsvektorene til henholdsvis A og B. Beregn hastigheten til B sett fra A.
Vtil = (3, -1, 5) Vb = (2, 5, -3)
I dette tilfellet blir den relative hastigheten til B med hensyn til A bedt om VB / A
VB / A = VB - VTIL
VB / A = (2, 5, -3) - (3, -1, 5) = (-1, 6, -8)
Dette er hastighetsvektoren til B sett fra A. Der en ny vektor med hastigheten til B er beskrevet med henvisning fra en observatør plassert ved A og beveger seg med hastigheten på A.
1-konstruer 3 vektorer A, B og C som er samtidig og relaterer 3 operasjoner mellom seg gjennom en praktisk øvelse.
2-La vektorene A: (-2, 4, -11), B: (1, -6, 9) og C: (-2, -1, 10). Finn vektorer vinkelrett på: A og B, C og B, Summen A + B + C.
4-Bestem 3 vektorer som er vinkelrette på hverandre, uten å ta hensyn til koordinataksene.
5-Definer arbeidet som utføres av en kraft som løfter en masseblokk på 5 kg, fra bunnen av en 20 m dyp brønn.
6-Vis algebraisk at subtraksjonen av vektorer er lik summen av den motsatte vektoren. Begrunn postulatene dine.
7-Betegn en vektor i alle notasjonene som er utviklet i denne artikkelen. (Kartesisk, polær, analytisk og sfærisk).
8-De magnetiske kreftene som utøves på en magnet som hviler på et bord, er gitt av følgende vektorer; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Bestem i hvilken retning magneten vil bevege seg hvis alle magnetiske krefter virker samtidig.
Ingen har kommentert denne artikkelen ennå.