
Gratisvektorer egenskaper, eksempler, øvelser
De gratis vektorer De er de som er fullstendig spesifisert av deres størrelse, retning og sans, uten at det er nødvendig å indikere et applikasjonspunkt eller en bestemt opprinnelse.
Siden uendelige vektorer kan tegnes på denne måten, er en fri vektor ikke en enkelt enhet, men et sett med parallelle og identiske vektorer som er uavhengige av hvor de er..
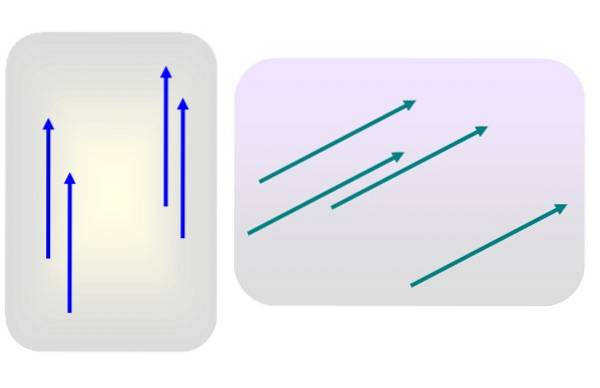
La oss si at vi har flere vektorer med styrke 3 rettet vertikalt oppover, eller av styrke 5 og tilbøyelig mot høyre, som i figur 1.
Ingen av disse vektorene brukes spesifikt på noe tidspunkt. Da er noen av de blå eller grønne vektorene representative for deres respektive gruppe, siden deres egenskaper - modul, retning og sans - ikke endres i det hele tatt når de overføres til et annet sted i planet..
En gratis vektor er for eksempel vanligvis betegnet i trykt tekst med en fet bokstav v. Eller med små bokstaver og en pil på toppen hvis det er håndskrevet tekst.
Artikkelindeks
- 1 Eksempler
- 1.1 Egenskaper og egenskaper
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2 Øvelse 2
- 3 Referanser
Eksempler
Fordelen med gratisvektorer er at de kan beveges gjennom planet eller gjennom rommet og opprettholde sine egenskaper, siden enhver representant for settet er like gyldig.
Derfor brukes de ofte i fysikk og mekanikk. For å indikere den lineære hastigheten til et fast stoff i bevegelse, er det ikke nødvendig å velge et bestemt punkt på objektet. Så hastighetsvektoren oppfører seg som en fri vektor.
Et annet eksempel på en fri vektor er kreftparet. EN par Den består av to krefter av like stor størrelse og retning, men av motsatte retninger, påført på forskjellige punkter på et fast stoff. Effekten av et par er ikke å oversette objektet, men å forårsake en rotasjon takket være øyeblikk produsert.
Figur 2 viser et par krefter påført et ratt. Gjennom kreftene F1 Y Fto, dreiemoment opprettes som roterer svinghjulet rundt midten og med klokken.
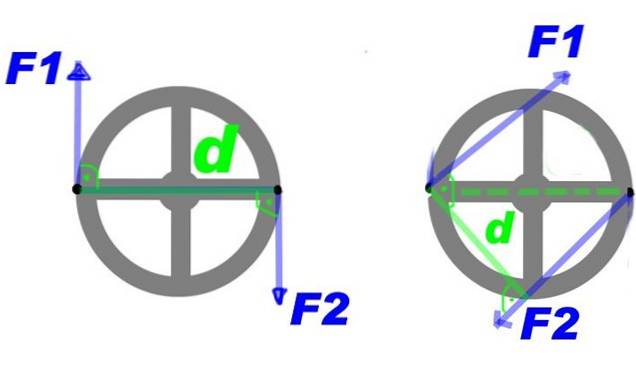
Du kan gjøre noen endringer i dreiemomentet og fremdeles få den samme roterende effekten, for eksempel å øke kraften, men redusere avstanden mellom dem. Eller oppretthold kraften og avstanden, men bruk dreiemomentet på et annet par punkter på rattet, det vil si rotere dreiemomentet rundt midten.
Øyeblikket til styrkerparet eller rett og slett par, er en vektor hvis modul er Fd og er rettet vinkelrett på svinghjulets plan. I eksemplet som vises ved konvensjon har rotasjonen med klokken en negativ følelse.
Egenskaper og egenskaper
I motsetning til gratisvektoren v, vektorene AB Y CD de er faste (se figur 3), siden de har et spesifisert startpunkt og ankomstpunkt. Men siden de er teammild med hverandre, og i sin tur med vektoren v, er representative for den gratis vektoren v.

Hovedegenskapene til gratisvektorer er følgende:
-Enhver vektor AB (se figur 2) er som sagt representativ for frivektoren v.
-Modulen, retningen og sansen er den samme i enhver representant for frivektoren. I figur 2, vektorene AB Y CD representerer gratisvektoren v og de er teamorienterte.
-Gitt et punkt P i rommet, er det alltid mulig å finne en representant for den gratis vektoren v hvis opprinnelse er i P, og representanten er unik. Dette er den viktigste egenskapen til gratisvektorer og den som gjør dem så allsidige.
-En nullfri vektor er betegnet som 0 y er settet med alle vektorer som mangler størrelse, retning og sans.
-Hvis vektoren AB representerer fri vektor v, deretter vektoren BA representerer fri vektor -v.
-Notasjonen vil bli brukt V3 å betegne settet med alle gratis vektorer av plass og Vto å utpeke alle gratisvektorer i flyet.
Løst øvelser
Med gratisvektorer kan følgende operasjoner utføres:
-Sum
-Subtraksjon
-Multiplikasjon av skalar med en vektor
-Skalarprodukt mellom to vektorer.
-Kryss produkt mellom to vektorer
-Lineær kombinasjon av vektorer
Og mer.
-Øvelse 1
En student prøver å svømme fra et punkt på bredden av en elv til et annet som er rett overfor. For å oppnå dette, ingenting direkte med en hastighet på 6 km / t, i en vinkelrett retning, men strømmen har en hastighet på 4 km / t som avbøyer den.
Beregn svømmerens resulterende hastighet og hvor mye han blir avbøyd av strømmen.
Løsning
Svømmerens resulterende hastighet er vektorsummen av hastigheten hans (med hensyn til elven, tegnet vertikalt oppover) og hastigheten til elven (tegnet fra venstre til høyre), som utføres som angitt i figuren nedenfor:
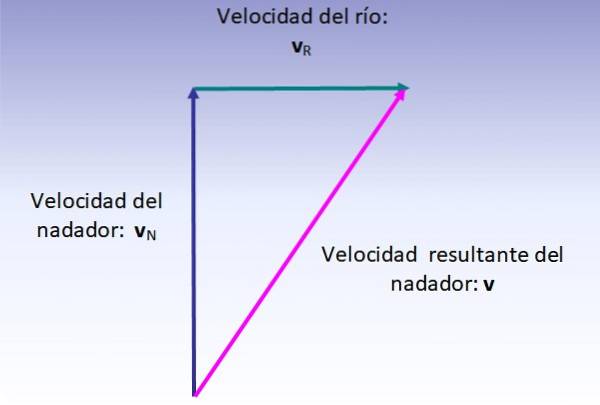
Størrelsen på den resulterende hastigheten tilsvarer hypotenusen til den rette trekanten vist, derfor:
v = (6to + 4to) ½ km / t = 7,2 km / t
Retningen kan beregnes ved hjelp av vinkelen i forhold til vinkelrett på kysten:
α = arctg (4/6) = 33,7º eller 56,3 ° i forhold til kysten.
Øvelse 2
Finn øyeblikket til paret vist i figuren:
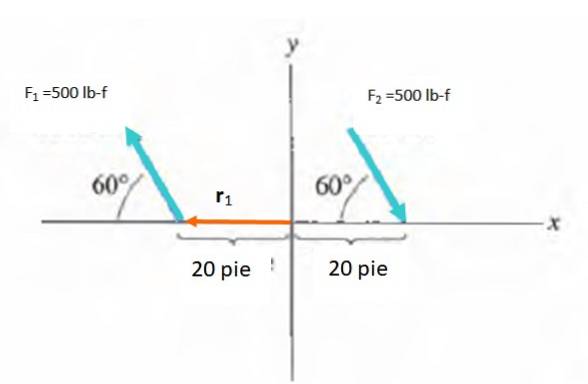
Løsning
Øyeblikket beregnes av:
M = r x F
Enhetene for øyeblikket er lb-f.ft. Siden dreiemomentet er i skjermplanet, rettes øyeblikket vinkelrett på det, enten utover eller innover..
Ettersom dreiemomentet i eksemplet har en tendens til å rotere objektet som det påføres (som ikke er vist på figuren) med klokken, anses dette øyeblikket å peke mot innsiden av skjermen med et negativt tegn.
Momentets størrelse er M = F.d. i a, hvor a er vinkelen mellom kraften og vektoren r. Du må velge et punkt som skal beregnes for øyeblikket, som er en fri vektor. Opprinnelsen til referansesystemet blir derfor valgt r går fra O til applikasjonspunktet for hver styrke.
M1 = Mto = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. fot
Nettomomentet er summen av M.1 og Mto: -17329,5 lb-f. fot.
Referanser
- Beardon, T. 2011. En introduksjon til vektorer. Hentet fra: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Volum 1. Kinematikk. 31-68.
- Fysisk. Modul 8: Vektorer. Gjenopprettet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Publishing Company. 15-53.
- Vector Addition Calculator. Gjenopprettet fra: 1728.org
- Vektorer. Gjenopprettet fra: en.wikibooks.org



Ingen har kommentert denne artikkelen ennå.