
Relativt hastighetskonsept, eksempler, øvelser
De relativ hastighet av et objekt er en som måles i forhold til en gitt observatør, siden en annen observatør kan oppnå en annen måling. Hastighet avhenger alltid av observatøren som måler den.
Derfor vil hastigheten til et objekt målt av en bestemt person være den relative hastigheten i forhold til det. En annen observatør kan oppnå en annen verdi for hastigheten, selv om det er det samme objektet.
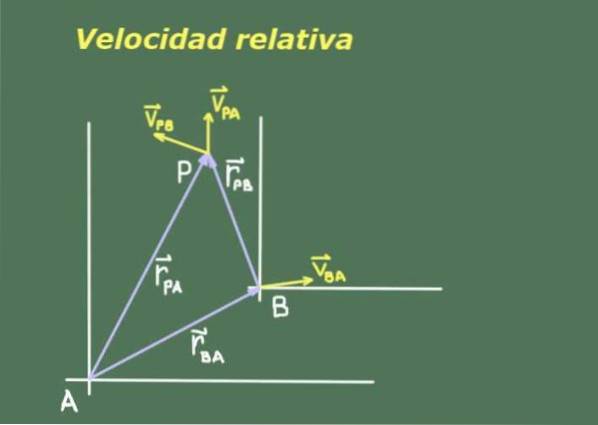
Siden to observatører A og B som beveger seg i forhold til hverandre, kan ha forskjellige målinger av et tredje objekt i bevegelse P, er det nødvendig å se etter et forhold mellom posisjonene og hastighetene til P sett av A og B.
Figur 1 viser to observatører A og B med sine respektive referansesystemer, hvorfra de måler posisjonen og hastigheten til objektet P.
Hver observatør A og B måler posisjonen og hastigheten til objektet P på et gitt øyeblikk t. I klassisk (eller galilensk) relativitetstid er tiden for observatør A den samme som for observatør B uavhengig av deres relative hastigheter.
Denne artikkelen handler om klassisk relativitet som er gyldig og anvendelig i de fleste hverdagssituasjoner der objekter har hastigheter som er mye langsommere enn lysets..
Vi betegner posisjonen til observatør B med hensyn til A som rBA. Siden posisjon er en vektormengde, bruker vi fet skrift for å indikere den. Posisjonen til objektet P i forhold til A er betegnet som rPA og det samme objektet P med hensyn til B rPB.
Artikkelindeks
- 1 Forholdet mellom relative posisjoner og hastigheter
- 1.1 Slik ser et barn det fra en bil i bevegelse
- 2 Relativ hastighet mellom motorsykkelen og bilen
- 2.1-Øvelse løst
- 3 Referanser
Forholdet mellom relative posisjoner og hastigheter
Det er et vektorforhold mellom disse tre posisjonene som kan trekkes fra representasjonen av figur 1:
rPA= rPB + rBA
Hvis derivatet av forrige uttrykk er tatt med hensyn til tid t vi vil oppnå forholdet mellom de relative hastighetene til hver observatør:
VPA= VPB + VBA
I det forrige uttrykket har vi den relative hastigheten til P i forhold til A som en funksjon av den relative hastigheten på P i forhold til B og den relative hastigheten på B i forhold til A.
Tilsvarende kan den relative hastigheten til P med hensyn til B skrives som en funksjon av den relative hastigheten til P med hensyn til A og den relative hastigheten til A med hensyn til B.
VPB= VPA + VAB
Det skal bemerkes at den relative hastigheten til A med hensyn til B er lik og i motsetning til den til B med hensyn til A:
VAB = -VBA
Slik ser et barn det fra en bil i bevegelse
En bil går på en rett vei, som går fra vest til øst, med en hastighet på 80 km / t mens en i motsatt retning (og fra den andre banen) kommer en motorsykkel med en hastighet på 100 km / t.
En gutt reiser på baksetet i bilen som vil vite den relative hastigheten til en motorsykkel som nærmer seg ham. For å finne ut svaret, vil barnet bruke forholdene som han nettopp har lest i forrige avsnitt, og identifisere hvert koordinatsystem som følger:
-A er koordinatsystemet til en observatør på veien, og i forhold til det har hvert kjøretøy blitt målt.
-B er bilen og P er motorsykkelen.
Hvis du vil beregne hastigheten på motorsykkel P med hensyn til bil B, vil følgende forhold bli brukt:
VPB= VPA + VAB=VPA - VBA
Tar vi vest-øst-retningen som positiv vi har:
VPB= (-100 km / t - 80 km / t) Jeg = -180 km / t Jeg
Dette resultatet tolkes slik: Motorsykkelen beveger seg relativt til bilen med en hastighet på 180 km / t og retning -Jeg, altså fra øst til vest.
Relativ hastighet mellom motorsykkelen og bilen
Motorsykkelen og bilen har krysset hverandre etter kjørefeltet. Barnet i baksetet på bilen ser motorsykkelen bevege seg bort og vil nå vite hvor fort den beveger seg bort fra ham, forutsatt at både motorsykkelen og bilen opprettholder de samme hastighetene som før den krysset..
For å vite svaret, bruker barnet det samme forholdet som ble brukt tidligere:
VPB= VPA + VAB=V PA - VBA
VPB= -100 km / t Jeg - 80 km / t Jeg = -180 km / t Jeg
Og nå beveger motorsykkelen seg vekk fra bilen med samme relative hastighet som den nærmet seg før de krysset..
Den samme motorsykkelen fra del 2 returneres med samme hastighet på 100 km / t, men endrer retning. Det vil si at bilen (som fortsetter med en hastighet på 80 km / t) og motorsykkelen begge beveger seg i positiv øst-vest retning..
På et bestemt tidspunkt passerer motorsykkelen bilen, og barnet i baksetet til bilen vil vite motorsykkelens relative hastighet i forhold til ham når han ser den passere..
For å få svaret, bruker barnet forholdet mellom relativ bevegelse igjen:
VPB= VPA + VAB=VPA - VBA
VPB= +100 km / t Jeg - 80 km / t Jeg = 20 km / t Jeg
Barnet fra baksetet ser motorsykkelen forbi bilen med en hastighet på 20 km / t.
-Treningen løst
Øvelse 1
En motorbåt krysser en elv som er 600 m bred og renner fra nord til sør. Elvens hastighet er 3 m / s. Båtens hastighet i forhold til elva vannet er 4 m / s mot øst.
(i) Finn hastigheten på båten i forhold til elvebredden.
(ii) Angi hastigheten og retningen til båten i forhold til land.
(iii) Beregn overgangstiden.
(iv) Hvor langt sør det vil ha beveget seg fra utgangspunktet.
Løsning
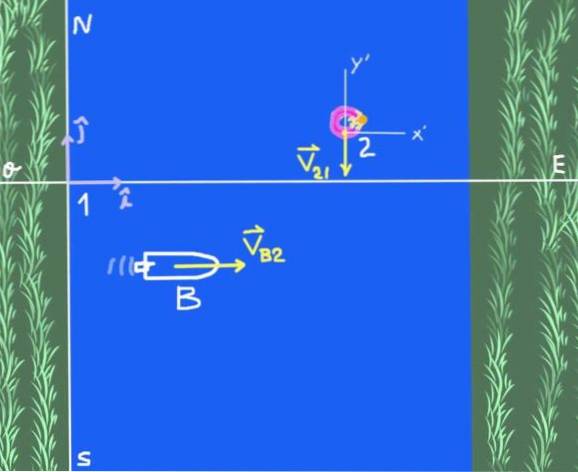
Det er to referansesystemer: det solidare referansesystemet på elvebredden som vi vil kalle 1 og referansesystemet 2, som er en observatør som flyter på elvevannet. Formålet med studien er båt B.
Båtens hastighet i forhold til elven er skrevet i vektorform som følger:
VB2 = 4 Jeg m / s
Hastigheten til observatør 2 (flåte på elven) med hensyn til observatør 1 (på land):
Vtjueen = -3 j m / s
Du vil finne hastigheten på båten i forhold til land VB1.
VB1 = VB2 + Vtjueen
Svar i
VB1 = (4 Jeg - 3 j) m / s
Hastigheten på båten vil være modulen til forrige hastighet:
|VB1| = (42 + (-3) 2) ½ = 5 m / s
Svar ii
Og adressen vil være:
θ = arctan (-¾) = -36,87º
Svar iii
Kryssetiden til båten er kvotienten mellom bredden på elven og x-komponenten av båtens hastighet i forhold til land.
t = (600m) / (4 m / s) = 150 s
Svar iv
For å beregne drift som båten hadde mot sør, multipliseres y-komponenten av båtens hastighet i forhold til land med kryssetiden:
d = -3 j m / s * 150 s = -450 j m
Forskyvningen mot sør i forhold til utgangspunktet er 450m.
Referanser
- Giancoli, D. Fysikk. Prinsipper med applikasjoner. 6. utgave. Prentice Hall. 80-90
- Resnick, R. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 100-120.
- Serway, R., Jewett, J. (2008). Fysikk for naturvitenskap og ingeniørfag. Volum 1. 7. Utgave. Mexico. Cengage Learning Editors. 95-100.
- Wikipedia. Relativ hastighet. Gjenopprettet fra: wikipedia.com
- Wikipedia. Relativ hastighetsmetode. Gjenopprettet fra: wikipedia.com



Ingen har kommentert denne artikkelen ennå.